 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы

Выражения вида `-4x^2+5x+7` носят название квадратного трёхчлена. В общем случае квадратным трёхчленом называют выражение вида где – произвольные числа, причём
Рассмотрим квадратный трёхчлен Запишем его в таком виде: Прибавим к этому выражению и вычтем получаем: Заметим, что поэтому
Преобразование, которое мы сделали, носит название «выделение полного квадрата из квадратного трёхчлена».
Выделите полный квадрат из квадратного трёхчлена
Заметим, что `3x=2*1/2*3x`. Тогда
`9x^2+3x+1=(3x)^2+2*1/2*3x+1`.
Прибавим и вычтем к полученному выражению `(1/2)^2`, получаем
`((3x)^2+2*1/2*3x+(1/2)^2)+1-(1/2)^2=(3x+1/2)^2+3/4`.
Покажем, как применяется метод выделения полного квадрата из квадратного трёхчлена для разложения квадратного трёхчлена на множители.
Разложите на множители квадратный трёхчлен
Выделяем полный квадрат из квадратного трёхчлена:
Теперь применяем формулу получаем:
Разложите на множители квадратный трёхчлен
Теперь замечаем, что
Прибавляем к выражению слагаемое получаем:
Применяем формулу для разности квадратов, имеем:
Разложите на множители квадратный трёхчлен
Мы не можем представить выражение как квадрат какого-то выражения, т. к. ещё не изучали этого в школе. Это будете проходить позже, и уже в Задании №4 будем изучать квадратные корни. Покажем, как можно разложить на множители заданный квадратный трёхчлен:
`3x^2-14x-5=3(x^2-14/3 x-5/3)=3(x^2-2*7/3 x+(7/3)^2-(7/3)^2-5/3)=`
`=3((x-7/3)^2-49/9-5/3)=3((x-7/3)^2-64/9)=3((x-7/3)^2-8/3)^2)=`
`=3(x-7/3-8/3)(x-7/3+8/3)=3(x-5)(x+1/3)=(x-5)(3x+1)`.
Покажем, как применяется метод выделения полного квадрата для нахождения наибольшего или наименьшего значений квадратного трёхчлена.
Рассмотрим квадратный трёхчлен Выделяем полный квадрат:
`(x)^2-2*x*1/2+(1/2)^2-(1/2)^2+3=(x-1/2)^2+11/4`. Заметим, что при `x=1/2` значение квадратного трёхчлена равно `11/4`, а при `x!=1/2` к значению `11/4` добавляется положительное число, поэтому получаем число, большее `11/4`. Таким образом, наименьшее значение квадратного трёхчлена равно `11/4` и оно получается при `x=1/2`.
Найдите наибольшее значение квадратного трёхчлена
Выделяем полный квадрат из квадратного трёхчлена:
При `x=1/4` значение квадратного трёхчлена равно а при `x!=1/4` из числа вычитается положительное число, то есть получаем число, меньшее Таким образом, число является наибольшим значением квадратного трёхчлена, и оно получается при `x=1/4`.
Разложите на множители числитель и знаменатель дроби `{x^2+2x-15}/{x^2-6x+9}` и сократите эту дробь.
Заметим, что знаменатель дроби Разложим числитель дроби на множители, применяя метод выделения полного квадрата из квадратного трёхчлена.
Данную дробь привели к виду `{(x+5)(x-3)}/(x-3)^2` после сокращения на получаем `(x+5)/(x-3)`.
Разложите многочлен на множители.
Применим к этому многочлену метод выделения полного квадрата.
`x^4-13x^2+36=(x^2)^2-2*x^2*13/2+(13/2)^2-(13/2)^2+36=`
`=(x^2-13/2)^2-169/4+36=(x^2-13/2)^2-25/4=`
`=(x^2-13/2)^2-(5/2)^2=(x^2-13/2-5/2)(x^2-13/2+5/2)=`
`=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)`.
Разложите на множители многочлен
Применяем метод выделения полного квадрата. Имеем:
Применяя метод выделения полного квадрата, разложите на множители числитель и знаменатель и сократите дробь `{8x^2+10x-3}/{2x^2-x-6}`.
`8x^2+10x-3=8(x^2+10/8 x-3/8)=8(x^2+2*5/8 x+(5/8)^2-(5/8)^2-3/8)=`
`=8((x+5/8)^2-25/64-24/64)=8((x+5/8)^2-(7/8)^2)=`
`=8(x+5/8+7/8)(x+5/8-7/8)=8(x+12/8)(x-2/8)=`
`=8(x+3/2)(x-1/4)=(2x+3)(4x-1)`.
Преобразуем знаменатель дроби:
`2x^2-x-6=2(x^2-x/2-6/2)=2(x^2-2*1/4 x+(1/4)^2-(1/4)^2-6/2)=`
`=2((x-1/4)^2-(7/4)^2)=2(x-1/4-7/4)(x-1/4+7/4)=`
`=2(x-2)(x+3/2)=(x-2)(2x+3)`.
Имеем: `{(2x+3)(4x-1)}/{(x-2)(2x+3)}={4x-1}/{x-2}`.

Равенство, содержащее переменную, называют уравнением с одной переменной или уравнением с одним неизвестным.
Например, уравнением с одной переменной является равенство $$ 2(3x+5)=4x-1.$$
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Например, число $$ 1$$ является решением уравнения $$ 3x+5=9x-1.$$ Уравнение $$ {x}^{2}+1=0$$ не имеет решений, т. к. левая часть уравнения всегда больше нуля. Уравнение $$ (x-1)(x+2)=0$$ имеет два корня: $$ {x}_{1}=1$$ и $$ {x}_{2}=-2.$$
Решить уравнение – значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если каждое решение первого уравнения является решением второго и каждое решение второго уравнения является решением первого или если оба уравнения не имеют решений.
При решении уравнений используют следующие свойства
1) если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение вида $$ ax=b,$$ где $$ x - $$переменная, $$ a$$ и $$ b - $$ некоторые числа, называется линейным уравнением с одной переменной.
Если $$ a\ne 0$$, то уравнение имеет единственное решение $$ x=\frac{b}{a}.$$
Если $$ a=0$$ и $$ b=0,$$ то уравнению удовлетворяет любое значение $$ x,$$ а если $$ a=0,$$ а $$ b\ne 0,$$ то уравнение не имеет решений, т. к. $$ 0·x=b$$ не выполняется ни при одном значении переменной.
Решите уравнение $$ \mathrm{2,5}x-(x+1)=(3x-1)-2x+1$$.
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с $$ x$$ в левую часть уравнения, а слагаемые, не содержащие $$ x,$$ в правую часть, получаем:
$$ \mathrm{2,5}x-x-3x+2x=1-1+1, $$
$$ \mathrm{0,5}x=1,$$ $$ x=2.$$
Решите уравнение:
а) $$ 2{x}^{2}-3x=0$$;
б) $$ {x}^{3}-2{x}^{2}-9x+18=0$$;
в) $$ {x}^{2}+5x+6=0$$.
а) Преобразуем уравнение: $$ x(2x-3)=0.$$ Произведение равно нулю, если один из сомножителей равен нулю, получаем $$ {x}_{1}=0,$$ $$ {x}_{2}=\frac{3}{2}.$$
б) Разложим на множители левую часть уравнения:
$$ {x}^{2}(x-2)-9(x-2)=(x-2)({x}^{2}-9)=(x-2)(x-3)(x+3).$$
Отсюда видно, что решениями этого уравнения являются числа $$ {x}_{1}=2,$$ $$ {x}_{2}=3,$$ $$ {x}_{3}=-3.$$
$$ 2; 3; -3.$$
в) Это уравнение называется квадратным, вы подробно изучите эти уравнения в 8-м классе. Но покажем, как можно решать такие уравнения. Представим $$ 5x$$ как $$ 2x+3x,$$ тогда имеем:
$$ {x}^{2}+2x+3x+6=0,$$
$$ x(x+2)+3(x+2)=0, (x+2)(x+3)=0,$$
отсюда видно, что $$ {x}_{1}=-2,$$ $$ {x}_{2}=-3.$$
Это уравнение можно решать и методом выделения полного квадрата. Представим выражение $$ 5x=2·\frac{5}{2}x.$$ И прибавим и вычтем в левой части уравнения число $$ \frac{25}{4},$$ получаем:
`x^2+2*5/2*x+25/4-25/4+6=0`,
`(x+5/2)^2-25/4+6=0`,
`(x+5/2)^2-1/4=0`,
`(x+5/2)^2-(1/2)^2=0`,
`(x+5/2-1/2)(x+5/2+1/2)=0`,
`(x+2)(x+3)=0`.
Откуда следует, что $$ {x}_{1}=-2$$ и $$ {x}_{2}=-3.$$
$$ -2; -3.$$
Являются ли данные уравнения равносильными:
а) $$ \left|x-1\right|=2$$ и $$ 2x-5=1;$$
б) $$ \frac{(x-3)(x+7)}{x-3}=0$$ и $$ (x-3)(x+7)=0.$$
а) Если $$ \left|x-1\right|=2,$$ то $$ x-1=2, x=3, $$или $$ x-1=-2, x=-1.$$ Первое уравнение имеет два решения: $$ -1$$ и $$ 3.$$
Второе уравнение имеет одно решение $$ x=3.$$ Число $$ \left(-1\right)$$ является решением первого уравнения и не является решением второго уравнения, следовательно, данные уравнения не являются равносильными.
б) Число $$ x=3$$ является решением второго уравнения и не является решением первого уравнения, т. к. при $$ x=3$$ не определена дробь, стоящая в левой части первого уравнения, поэтому данные уравнения не являются равносильными.

Если число положительное, то его модуль равен самому числу. Например, `|2,5|=2,5`; `|1 3/4|=1 3/4`.
Если число отрицательное, то его модуль равен противоположному числу. Например, `|-3,1|=3,1`; `|-2 3/7|=2 3/7`.
Модуль нуля равен нулю.
Запишем определение модуля таким образом: $$\left | x \right |= \left\{\begin{matrix}
x, если {} x\geq 0,\\
-x, если {} x<0.
\end{matrix}\right.$$
Докажем некоторые свойства модуля.
Для любого числа $$ x$$ выполняется условие $$ \left|x\right|\ge 0$$.
Действительно, если $$ x>0$$, то $$ \left|x\right|=x$$ и тогда $$ \left|x\right|>0$$.
Если $$ x<0$$, то $$ \left|x\right|=-x$$, но $$ -x>0$$, значит $$ \left|x\right|>0$$. И если $$ x=0$$, то $$ \left|x\right|=0$$.
Таким образом, $$ \left|x\right|\ge 0$$ для любого $$ x$$. При этом заметим, что $$ \left|x\right|>0$$, если $$ x\ne 0$$, и $$ \left|x\right|=0$$, если $$ x=0$$.
При каких значениях $$ x$$ выполняются равенства:
а) $$ \left|x\right|=5$$ ;
б) $$ \left|x\right|=-3$$;
в) $$ \left|x-1\right|=2$$?
Решение
б) По свойству $$ 1$$ выполняется условие $$ \left|x\right|\ge 0$$, а у нас условие $$ \left|x\right|=-3<0$$. Следовательно, не существует чисел, для которых выполнялось бы данное условие.
в) По определению модуля числа следует, что если $$ x-1\ge 0$$, т. е. $$ x\ge 1$$, то $$ \left|x-1\right|=x-1=2$$, отсюда следует, что $$ x=3$$. Если же $$ x<1$$, то $$ x-1<0$$ и $$ \left|x-1\right|=-(x-1)$$, получаем равенство $$ -x+1=2$$, $$ -x=1$$, $$ x=-1$$. В дальнейшем мы такие уравнения будем решать коротко, а именно, рассуждаем так: если модуль какого-то выражения равен $$ 2$$, то либо это выражение равно $$ 2$$, либо равно $$ (-2)$$. Если $$ \left|x-1\right|=2$$, то получаем два случая: $$ x-1=2$$, $$ x=3$$ и $$ x-1=-2$$, $$ x=-1$$.
Для любых чисел $$ x$$ и $$ y$$ выполняется условие
$$ \left|xy\right|=\left|x\right|·\left|y\right|$$.
Если числа $$ x$$ и $$ y$$ положительные, то $$ xy>0$$, $$ \left|xy\right|=xy$$, $$ \left|x\right|=x$$, $$ \left|y\right|=y$$, получаем верное равенство $$ xy=xy$$.
Если числа $$ x$$ и $$ y$$ отрицательные, то $$ xy>0$$, $$ \left|xy\right|=xy$$, $$ \left|x\right|=-x$$, $$ \left|y\right|=-y$$, получаем верное равенство $$ xy=(-x)(-y)$$, $$ xy=xy$$.
Если $$ x>0$$, а $$ y<0$$, то $$ xy<0$$, $$ \left|xy\right|=-xy,$$ $$ \left|x\right|=x$$, $$ \left|y\right|=-y$$, получаем верное равенство $$ -xy=-xy$$.
Аналогично доказывается, если $$ x<0$$, a $$ y>0$$.
Если одно из чисел $$ x$$ и $$ y$$ равно нулю, то обе части равенства $$ \left|xy\right|=\left|x\right|·\left|y\right|$$равны нулю, т. е. равенство верное.
При каких значениях $$ x$$ верно равенство $$ \left|-5x-10\right|=15$$.
$$ x+2=3$$, $$ x=1$$ и $$ x+2=-3$$, $$ x=-5$$.
$$ 1$$; $$ -5$$.
Аналогично свойству $$ 2$$ можно доказать свойство `|x/y|=|x|/|y|`. Исходя из определения модуля числа, можно доказать, что для любого числа $$ x$$ верно равенство $$ \left|x\right|=\left|-x\right|$$.
Решите уравнение `|-3x-1|-2x=2`.
`|-3x-1|=|-3(x+1/3)|=|-3|*|x+1/3|=3|x+1/3|`.
После этих преобразований получили уравнение `3*|x+1/3|-2x=2`.
Из определения модуля следует, что `|x+1/3|=x+1/3`, если `x+1/3>=0`, т. е. `x>=-1/3` и `|x+1/3|=-x-1/3`, если `x<-1/3`.
а) Если `x>=-1/3`, то получаем уравнение `3(x+1/3)-2x=2`, `x+1=2`, `x=1`. Число `1> -1/3`, поэтому число `x=1` является решением уравнения.
б) Если `x<-1/3`, то получаем уравнение `3(-x-1/3)-2x=2`, `-5x=3`, `x=-3/5<-1/3`.
Решите уравнение $$ \left|x-1\right|+\left|x+1\right|=2$$.
Напомним определение модуля числа: $$ \left|a\right|=\left\{\begin{array}{l}a, a\ge 0,\\ -a, a<0.\end{array}\right.$$
В данном уравнении под знаком модуля стоят числа $$ x-1$$ и $$ x+1.$$
Если $$ x$$ меньше, чем $$ -1,$$ то число $$ x+1$$ отрицательное, тогда $$ \left|x+1\right|=-x-1.$$
А если $$ x>-1,$$ то $$ \left|x+1\right|=x+1.$$ При $$ x=-1$$ имеем $$ \left|x+1\right|=0.$$ Таким образом, $$ \left|x+1\right|=\left\{\begin{array}{l}x+1, x\ge -1,\\ -x-1, x<-1.\end{array}\right.$$
Аналогично $$ \left|x-1\right|=\left\{\begin{array}{l}x-1, x\ge 1,\\ -x+1, x<1.\end{array}\right.$$
а) Рассмотрим наше уравнение при $$ x\le -1,$$ оно равносильно уравнению $$ -x+1-x-1=2,$$ $$ -2x=2,$$ $$ x=-1.$$ Это число принадлежит множеству $$ x\le -1.$$
б) Пусть теперь `-1<x<=1`, тогда данное уравнение равносильно уравнению `-x+1+x+1=2`, `0*x=0`, последнему уравнению удовлетворяет любое число, но так как мы рассматриваем множество `-1<x<=1`, значит, этому уравнению удовлетворяют все числа из этого множества.
в) Рассмотрим случай `x>1`. Уравнение равносильно уравнению `x-1+x+1=2`, `x=1`. Число `x=1` мы получили уже в пункте б).
Ответ
Решите уравнение: $$ \left|11x+5\right|=\left|9x+13\right|.$$
Если модули чисел равны, то эти числа либо равны, либо отличаются знаком. Если числа равны, то получаем уравнение:
$$ 11x+5=9x+13,$$ $$ 2x=8,$$ $$ x=4.$$
Если числа отличаются знаком, то получаем уравнение:
$$ 11x+5=-9x-13,$$ $$ 20x=-18,$$ $$ x=-\mathrm{0,9}.$$
Решите уравнение: $$ \left|5-\left|x+6\right|\right|+1=6$$.
Перенесём `1` в правую часть, получим $$ \left|5-\left|x+6\right|\right|=5$$. Теперь по определению модуля рассмотрим два случая: `5-|x+6|=5` и `5-|x+6|=-5`.
Решим каждое из них. `-|x+6|=5-5`, `|x+6|=0`, если модуль равен нулю, то выражение под модулем равно нулю `|x+6|=0`, `x=-6`.
Решим второе уравнение: `-|x+6|=-10`, `|x+6|=10`, опять получим два случая: `x+6=10` и `x+6=-10`. Решим их: `x=4` и `x=-16`.

Рассмотрим уравнение Такие уравнения носят название «уравнения с параметром». Здесь - неизвестное , а - параметр. Требуется найти решение при любых значениях параметра
Если то уравнение принимает вид: этому уравнению удовлетворяет любое число т. е. в этом случае уравнение имеет бесконечно много решений.
Если то уравнение принимает вид: это уравнение не имеет решений.
Если и то обе части уравнения можно разделить на тогда получаем: `x={(a-3)(a+5)}/{(a-3)(a-2)}={a+5}/{a-2}`. Таким образом, если и то уравнение имеет единственное решение и при этом `x={a+5}/{a-2}`.
Найдите значение параметра `a`, при котором уравнение `|x+a|=a-4` имеет один корень.
Для того чтобы уравнение имело один корень необходимо чтобы правая часть была равна нулю: `a-4=0`, то есть `a=4`.
При `a=4` уравнение имеет один корень.
Найдите значение параметра `a`, при котором уравнение `(a-2)x=2` не имеет корней.
Если `a=2`, то уравнение принимает вид: `0*x=2`, это уравнение не имеет решений.
При `a=2` уравнение не имеет корней.
Найдите целые значения параметра `a`, при которых корень уравнения `ax=-8` удовлетворяет неравенству `1,5<|x|<4`.
Из уравнения `x=-8/a`, `1,5<|-8/a|<4`, `a=4`, `a=-4`, `a=3`, `a=-3`, `a=5`, `a=-5`.

Функция вида $$ y=kx+b$$, где `k` и `b` - произвольные числа, называется линейной функцией. Графиком линейной функции является прямая.
Рассмотрим частные случаи функции `y=kx+b`, когда `k` и (или) `b` принимают значения равные нулю:
1) если `b=0`, то прямая пропорциональность, график проходит через начало координат;
2) если` k=0`, то `y=b`, графиком является прямая, параллельная оси `Ox`;
3) если `b=0`, `k=0`, то `y=0`, то графиком является ось `Ox`.
Для построения графика достатояно указать две точки, принадлежащие прямой, и затем через эти две точки провести прямую.
Постройте график функции: а) $$ y=2x+3$$; б) $$ y=2$$.
а) При $$ x=0$$; $$ y=3$$; при $$ x=1$$; $$ y=5$$. Проводим прямую через точки $$ (0; 3)$$ и $$ (1; 5)$$. График прямой приведён на рисунке 1.
б) Для любого значения $$ x$$ значение $$ y=2$$. Графиком этой функции является прямая, параллельная оси $$ Ox$$ и проходящая через точку $$ (0; 2)$$. График этой функции приведён на рисунке 2.
График линейной функции `y=kx+b`, где `k` и `b` - произвольные числа, может быть получен из графика функции `y=kx` путём его параллельного переноса вдоль оси `Oy` на `b` единиц вверх, если `b` - положительно, или `|b|` единиц вниз, если `b` - отрицательно.
В примере 1а) `y=2x+3`, при построении графика можно сначала построить график функции `y=2x`, а затем параллельным переносом вдоль оси `Oy` на `3` единицы вверх перенести график (рис. 3).
Число `k` называют угловым коэффициентом прямой – графика функции `y=kx+b`. Если `k>0` то угол наклона прямой `y=kx+b` к оси `x` острый; если `k<0` то угол наклона тупой.
Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются, а если угловые коэффициенты одинаковы, то прямые параллельны.
Построим теперь график функции $$ y=\left|x\right|$$.
Из определения модуля числа следует, что $$ y=\left\{\begin{array}{c}x, \mathrm{если} x>0,\\ 0, \mathrm{если} x=0,\\ -x, \mathrm{если} x<0.\end{array}\right.$$
При $$ x\ge 0 y=x$$, графиком функции при $$ x\ge 0$$ является часть прямой $$ y=x$$. А при $$ x<0$$ графиком функции является часть прямой $$ y=-x$$. График функции $$ y=\left|x\right|$$ приведён на рисунке 3а.
Постройте график функции $$ y=\left|x+1\right|-\left|x-2\right|$$.
Выражение $$ x-2$$ равно нулю при $$ x=2$$. Если $$ x>2$$, то $$ x-2>0$$, поэтому $$ \left|x-2\right|=x-2$$. А если $$ x<2$$, то $$ x-2<0$$, тогда $$ \left|x-2\right|=-(x-2)=-x+2$$. Выражение $$ x+1$$ равно нулю, если $$ x=-1$$.
Если $$ x>-1$$, то $$ x+1>0$$, тогда $$ \left|x+1\right|=x+1$$.
А если $$ x<-1$$, то $$ x+1<0$$, тогда $$ \left|x+1\right|=-(x+1)=-x-1$$. Пусть $$ x\ge 2$$, тогда $$ \left|x-2\right|=x-2$$, $$ \left|x+1\right|=x+1$$, поэтому $$ y=x+1-(x-2)=3$$.
Если , то , , тогда .
Если $$ x\le -1$$, то , , тогда .
Таким образом,
Заметим, что прямая $$ y=2x-1$$ проходит через точки $$ (-1; -3)$$ и $$ (2; 3)$$. График данной функции приведён на рисунке 4.
Постройте график функции $$ y=\left\{\begin{array}{l}\left|x-3\right|, x\ge 0;\\ \left|x+4\right|-1, \text{если} x<0.\end{array}\right.$$
Используя график функции, определите, сколько будет точек пересечения графика функции с прямой $$ y=a$$ при различных значениях параметра $$ a$$.
Далее $$ \left|x+4\right|-1=\left\{\begin{array}{l}-4-x-1,\text{ если} x\le -4;\\ 4+x-1, \text{если} x\in (-4; 0).\end{array}\right.$$
График данной функции приведён на рисунке 5.
Если $$ a<-1$$, то прямая $$ y=a$$ не пересекает график данной функции.
Если $$ a=-1$$, то прямая пересекает график функции в точке $$ (-4; -1)$$.
Если $$ a\in (-1; 0)$$, то будет две точки пересечения.
Если $$ a=0$$, то прямая $$ y=0$$ пересекает график функции в точках $$ (-5; 0)$$, $$ (-3; 0)$$, $$ (3; 0)$$.
Если $$ a\in (0; 3)$$, то получается $$ 4$$ точки пересечения.
Если $$ a=3$$, то будет $$ 3$$ точки пересечения.
Если $$ a>3$$, то будет $$ 2$$ точки пересечения.

Дорогие ребята! Поздравляем вас с поступлением в заочную физико-техническую школу МФТИ. Вы получили первое задание по математике, в нем мало сложных задач, советуем вам внимательно изучить разработку, без ошибок ответить на контрольные вопросы и постараться решить предложенные вам задачи. Мало знать, как решить задачу, главное – уметь довести решение до конца и при этом не допустить арифметических ошибок. Не огорчайтесь, если вы не сможете справиться со всеми задачами. Вам вышлют решение задания, вы сможете посмотреть, как следует решать ту или иную задачу. В некоторых задачах мы указываем название учебного заведения (например, МГУ или МФТИ). Это означает, что данная задача предлагалась на вступительных экзаменах.
Обратите внимание, как оформлены решения в присланных вам заданиях и как записывают решения задач в ваших учебниках и задачниках.
Грамотный человек должен быть грамотным во всех предметах. Не забывайте о правилах грамматики, особенно о точках и запятых в ваших решениях. Постарайтесь аккуратно оформлять ваши решения.
Мы очень надеемся, что поможем вам в изучении математики. Рады будем видеть вас в будущем студентами нашего института.
Желаем вам больших успехов в этом году!

Одна из замечательных теорем геометрии, доказательство которой вам уже известно по учебнику, гласит: «сумма углов треугольника равна `180^@`». Как вы думаете, можно ли было установить этот факт экспериментально?
| Рис. 1 | Рис. 2 |
Предположим, что мы будем измерять угол, равный сумме углов треугольника, транспортиром. Нарисуем некоторый треугольник, приложим транспортир к одному из углов – углу `1`, отметим его величину, затем приложим транспортир к другому углу (рис. 1), отметим величину суммы двух углов, затем приложим транспортир к третьему углу. Мы обнаружим, что третья отметка придётся на `180^@`. Следует ли из наших измерений, что сумма углов рассмотренного треугольника точно равна `180^@`? А может быть больше на `1//10` градуса или меньше на `2//15` градуса? Такую разницу, как бы тщательно мы ни проводили измерения с помощью транспортира, заметить невозможно.
Кроме того, любой нарисованный треугольник, можно сказать, имеет «дефект»: как бы тонок ни был карандаш, которым его рисовали, стороны треугольника, если рассмотреть рисунок в увеличительное стекло, предстанут перед нами широкими неровными полосами. Какой же угол мы измеряли? Поэтому сомнения в точности наших измерений ещё более возрастут, и вывод может быть сделан только такой: сумма углов треугольника на рис. 1 близка к .
Предположим, что аналогичные измерения мы провели в каждом из треугольников, изображённых на рис. 2, и получили такие же результаты. Тогда мы можем предположить, выдвинуть гипотезу, что в любом нарисованном треугольнике сумма углов близка к `180^@`. Но даже такую гипотезу проверить экспериментально не представляется возможным, т. к.пришлось бы провести измерения во всех разнообразных треугольниках, т. е. в бесконечном числе случаев, что, конечно, неосуществимо.
Мы привели эти рассуждения, чтобы обратить ваше внимание на следующие важные моменты. Попытки экспериментально установить свойства фигур неосуществимы по ряду причин: из-за бесконечного разнообразия видов фигур, из-за «дефектности» самих фигур и, наконец, из-за неизбежных ошибок измерения.
В науке геометрии рассматриваются не реальные, конкретные фигуры, вырезанные из картона, нарисованные на листе бумаги и т.п., а идеальные, как говорят, абстрактные фигуры, которые целиком описываются только своими определениями. Реальные треугольники имеют не только форму и размер, они могут быть сделаны из картона или жести, бумаги или дерева и т. п. Отвлекаясь от всех их свойств, кроме формы и размера, т. е. выделяя общее для всех таких фигур, приходят к представлению о геометрическом треугольнике как фигуре, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Только для абстрактных геометрических фигур удается установить ряд простых и важных свойств. Именно для абстрактных геометрических треугольников справедливо утверждение, что сумма углов в каждом из них равна `180^@`. Истинность этого утверждения, как и других утверждений, называемых теоремами, устанавливается методом строгих рассуждений, основанных на логике и вытекающих из ранее доказанных утверждений. Как вы сами убедились, эти рассуждения столь убедительны, что с ними соглашается всякий, рассмотревший их.
Метод строгих геометрических доказательств, основанных на логике, когда одно утверждение вытекает из ранее установленного, является основным методом в геометрии. В этом смысле геометрию называют дедуктивной наукой, от латинского слова deductio – выведение.
Если разобрать вывод, т. е. доказательство какой-нибудь геометрической теоремы, то он логически следует из ранее доказанных теорем. Для этих ранее доказанных теорем, в свою очередь, можно выделить те факты, из которых они выводятся и которые были установлены ранее.
Но ведь есть какое-то первое утверждение, которое не вытекает из ранее доказанного, так как вообще нет теорем, которые уже были доказаны до этого. Это означает, что некоторые факты должны быть приняты без доказательства. Их называют аксиомами, от греческого – удостоенное, принятое положение.
Так же обстоит дело с определениями геометрических объектов. Вводя новое определение, пользуются определениями и понятиями, которые уже были введены раньше. Но как быть с первым определением? Через что его определить, если еще нет понятий, определенных ранее? Отсюда следует, что некоторые геометрические понятия должны быть введены без каких-либо определений. Такие неопределяемые понятия называются основными. В изучаемом курсе геометрии таковы понятия точки, прямой, плоскости.
Итак, все здание геометрии строится, во-первых, на основных неопределяемых понятиях, и, во-вторых, на аксиомах, в которых устанавливаются связи и взаимоотношения между первоначальными понятиями; затем с помощью определений вводятся новые понятия, для которых, исходя из первоначальных фактов, содержащихся в аксиомах, доказываются, выводятся с помощью логики, дальнейшие факты – теоремы.
Подобное строение какой-нибудь области математики называют аксиоматическим. Таким образом, геометрия – аксиоматическая наука.
Из всего сказанного вывод такой: хотите освоить науку геометрию (хотя бы в рамках школьной программы) – разберите аксиомы, учите определения и формулировки теорем, с которыми вас постепенно знакомит учебник, наизусть, как стихи. А умение рассуждать, доказывать, умение применять теорию в решении задач приходят постепенно. Этому способствуют разбор доказательств теорем из учебника (за две с лишним тысячи лет математики отобрали самые лучшие и простые доказательства – именно их вам приводят в учебнике), разбор решений характерных задач, овладение методами решений.
Гипотеза – от греческого – под, внизу и – положение, утверждение – предположительное суждение о закономерной связи явлений.
Абстракция – от латинского abstractio – отвлечение.
Теорема – от греческого рассматриваю.

Для повторения мы выбрали эти темы. Приводить доказательство теорем, содержащихся в учебнике, не будем, лишь напомним основные теоремы. Также обсудим некоторые важные вопросы, приведём примеры решения задач, докажем несколько дополнительных теорем (Всякое утверждение, сформулированное в общем виде и доказанное, есть теорема, но их так много и они часто столь просты, что наполнять ими учебник не имеет смысла, а вот учиться на них применению основных теорем, умению рассуждать, делать выводы, - очень полезно). Такие теоремы мы будем называть леммами.
В учебнике доказаны три признака равенства треугольников.
Первый признак: по двум сторонам и углу между ними.
Второй признак: по стороне и прилежащим к ней углам.
Третий признак: по трём сторонам.
Мы напомнили их краткую формулировку.
Отметим также важный момент. Запись равенства треугольников $$ △ABC=△KPM$$ означает: $$ \angle A=\angle K$$, $$ \angle B=\angle P$$, $$ \angle C=\angle M$$, $$ AB=KP$$, $$ AC=KM$$ и $$ BC=PM$$, т. е. соответствующие вершины стоят на соответствующих местах.
Когда это удобно, будем использовать обозначения: в треугольнике $$ ABC$$ углы обозначать $$ A$$, $$ B$$ и $$ C$$,
$$ a$$, $$ b$$ и $$ c$$ – стороны, противолежащие углам $$ A$$, $$ B$$ и $$ C$$,
$$ {h}_{a}$$, $$ {h}_{b}$$, $$ {h}_{c}$$ – высоты к сторонам $$ a$$, $$ b$$ и $$ c$$,
$$ {m}_{a}$$, $$ {m}_{b}$$, $$ {m}_{c}$$ – медианы к сторонам $$ a$$, $$ b$$ и $$ c$$.
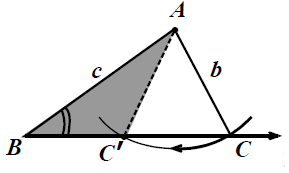
Покажем, как важно точно помнить формулировки теорем. Пусть треугольники $$ ABC$$ и `A^'B^'C^'` таковы, что `b^'=b`, `c^'=c` и `/_B^'=/_B`. Будут ли эти треугольники равны? Есть первый признак равенства «по двум сторонам и углу», но «углу между ними», а здесь какой угол? Нарисуем некоторый треугольник $$ ABC$$ (рис. 3) и отметим стороны и угол, о которых идёт речь: это не тот угол!
 |
||
| Рис. 3 | Рис. 4 | Рис. 5 |
Приведём пример треугольника `A^'B^'C^'` (рис. 5), который не равен треугольнику $$ ABC$$ `(B^'C^'!=BC)`, хотя `c=c^'`, `b=b^'` и `/_B=/_B^'`.
Рисунок 4 поясняет, как треугольник `A^'B^'C^'` получается из треугольника $$ ABC$$.
Приведём ещё пример (рис. 6), который показывает, что слова «прилежащим к стороне» чрезвычайно важны в формулировке второго признака равенства треугольников.
Здесь $$ AB={A}_{1}{B}_{1}$$, $$ \angle C=\angle {A}_{1}=90°$$, $$ \angle B=\angle {B}_{1}=45°$$
| Рис. 6 |
(Сторона одного треугольника равна стороне другого, два угла первого равны двум углам второго).
Но равные углы не прилежат к равным сторонам и `DeltaABC!=DeltaA_1B_1C_1`. Как легко видеть, треугольник $$ ABC$$ равен треугольнику $$ {A}_{1}{B}_{1}D$$ который составляет часть треугольника $$ {A}_{1}{B}_{1}{C}_{1}$$.
Треугольники $$ ABC$$ и `A^'B^'C^'` таковы, что равны их медианы, проведённые из вершин `B` и `B^'` и равны углы, которые образуют эти медианы со сторонами $$ a$$ и $$ c$$ и со сторонами `a^'` и `c^'` соответственно. Доказать, что `DeltaABC=DeltaA^'B^'C^'`.
Решение
При доказательстве мы рисуем треугольники, о которых идёт речь, в наиболее удобном положении (см. рис. 7), что возможно по аксиоме «перемещения треугольника», иначе называемой аксиомой «существования треугольника, равного данному».
| Рис. 7 |
Итак, $$ AM=CM$$, `A^'M^'=C^'M^'`, `BM=B^'M^'` равные углы $$ ABM$$ и `A^'B^'M^'` обозначим $$ \alpha $$ вторую пару равных углов обозначим $$ \phi $$.
1. В треугольнике $$ ABC$$ продолжим медиану $$ BM$$ за точку $$ M$$ и на прямой $$ BM$$ отложим отрезок $$ MD=BM$$. Рассмотрим треугольники $$ ABM$$ и $$ CDM$$.
Имеем: $$ AM=CM$$ (т. к. `BM` – медиана),
$$ BM=DM$$ (по построению),
$$ \angle AMB=\angle CMD$$ (как вертикальные).
По первому признаку равенства треугольников $$ △ABM= △CDM$$ В равных треугольниках против равных углов лежат равные стороны $$ (AB=CD)$$ и против равных сторон лежат равные углы (поэтому $$ \angle CDM=\alpha $$).
Аналогичное построение осуществим с треугольником `A^'B^'C^'` получим, что `A^'B^'=C^'D^'` и `/_C^'D^'M^'=alpha`.
2. Теперь рассмотрим треугольники $$ BCD$$ и `B^'C^'D^'`. Так как `BD=B^'D^'` и прилежащие к отрезкам $$ BD$$ и `B^'D^'` углы соответственно равны $$ \phi $$ и $$ \alpha $$, то `Delta BCD=DeltaB^'C^'D^'` по второму признаку равенства. Из этого равенства следует `CD=C^'D^'` (т. е. `c=c^'`) и `BC=B^'C^'` (т. е. `a=a^'`).
3. Вновь рассматриваем треугольники $$ ABC$$ и `A^'B^'C^'` Угол при вершине $$ B$$ равен углу при вершине `B^'` и равны стороны, образующие этот угол. По первому признаку равенства `Delta ABC=Delta A^'B^'C^'`.
На сторонах $$ AB$$ и $$ AD$$ квадрата $$ ABCD$$ во вне его построены равносторонние треугольники $$ AKB$$ и $$ AMD$$ (рис. 8). Доказать, что треугольник $$ KCM$$ также равносторонний.
Решение
Обозначим сторону квадрата $$ a$$ очевидно, что стороны равносторонних треугольников тоже равны $$ a$$. Отметим равные стороны в треугольниках $$ KBC$$, $$ CDM$$ и $$ KAM$$.
| Рис. 8 |
$$ △KBC=△CDM$$ по первому признаку, т. к. $$ \angle KBC=\angle CDM=90°+60°=150°$$.
Пусть прямая $$ CA$$ пересекает отрезок $$ KM$$ в точке $$ F$$.
$$ \angle KAC=\angle MAC=60°+45°=105°$$
Смежные с ними углы $$ KAF$$ и $$ MAF$$ равны $$ 180°-105°=75°$$ значит `/_RAM=150^@`, и $$ △KAM=△KBC$$ Делаем вывод: $$ KC=CM=KM$$ т. е. треугольник $$ KCM$$ – равносторонний.
(В решении использовано утверждение, что все углы равностороннего треугольника равны $$ 60°$$).
II. Равнобедренный треугольник.
В учебнике доказаны теоремы:
Т1. В равнобедренном треугольнике углы при основании равны.
Т2. В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.
Т3. (Признак равнобедренного треугольника). Если два угла в треугольнике равны, то он равнобедренный.
Обратим внимание, что признаком фигуры $$ A$$ называется теорема с формулировкой: «если имеет место … , то это фигура $$ A$$». Сформулируем следующие, часто применяемые в задачах, признаки равнобедренного треугольника:
а) если в треугольнике высота является медианой, то треугольник равнобедренный;
б) если в треугольнике высота является биссектрисой, то треугольник равнобедренный;
в) если в треугольнике медиана является биссектрисой, то треугольник равнобедренный.
Доказательство признака а) вполне простое. Если $$ BD\perp AC$$ и $$ AD=DC$$ (рис. 9), то $$ △ADB=△CDB$$ по двум сторонам ( $$ BD$$ – общая, $$ AD=DC$$) и углу между ними ($$ \angle ADB$$ смежный с $$ \angle BDC=90°$$ поэтому $$ \angle ADB=90°$$ ).
Из равенства треугольников следует $$ AB=BC$$ и треугольник $$ ABC$$ по определению равнобедренный.
| Рис. 9 | Рис. 10 |
Доказательство признака б) Столь же простое, докажите его самостоятельно.
Докажем признак в) Пусть в треугольнике $$ ABC$$ биссектриса $$ BM$$ является медианой: $$ AM=MC$$ (рис. 10). На продолжении биссектрисы $$ BM$$ отложим отрезок $$ MD$$ равный $$ BM$$ Треугольники $$ ABM$$ и $$ CDM$$ равны по первому признаку: у них углы при вершине $$ M$$ равны, как вертикальные, и $$ AM=CM$$, $$ BM=DM$$ Из равенства треугольников следует
$$ CD=AB$$ (1)
и $$ \angle CDM=\angle ABM$$. Но $$ \angle ABM=\angle CBM$$ поэтому $$ \angle CDM=\angle CBM$$, т. е. в треугольнике $$ BCD$$ углы при основании $$ BD$$ равны. По признаку Т3 этот треугольник равнобедренный: $$ BC=CD$$ Отсюда и из (1) заключаем: $$ BC=AB$$. Утверждение доказано.
В следующем примере применяются признак параллельности прямых и две теоремы об углах треугольника (и следствия этих теорем):
Т. Сумма углов треугольника равна $$ 180°$$.
Т. Внешний угол треугольника равен сумме двух внутренних углов, не
смежных с ним.
Точка $$ K$$ лежит на основании $$ AC$$ равнобедренного треугольника $$ ABC$$ ($$ AB=BC$$). Через точку $$ K$$ проведена прямая, пересекающая прямую $$ AB$$ и отрезок $$ BC$$, при этом образовалось два равнобедренных треугольника (рис. 11).
Найти углы треугольника $$ ABC$$.
Решение
Обозначим точки пересечения $$ M$$ и $$ D$$.
1. Углы при основании равнобедренного треугольника равны и они острые, значит угол $$ MAK$$ – тупой.
2. В треугольнике может быть только один тупой угол, значит, если треугольник $$ MAK$$ равнобедренный, то равными могут быть только углы при вершинах $$ M$$ и $$ K$$. Обозначим их $$ \alpha $$.
3. $$ \angle BAK=2\alpha $$ (как внешний угол треугольника $$ MAK$$), $$ \angle BCA=2\alpha $$ (углы при основании равнобедренного треугольника равны) и $$ \angle DKC=\alpha $$ ($$ \angle DKC=\angle AKM$$ как вертикальные).
Расставим углы.
4. Треугольник $$ KDC$$ по условию равнобедренный. Возможны, вообще говоря, два случая: а) $$ \angle KDC=\alpha $$ и б) $$ \angle KDC=2\alpha $$.
а) Если $$ \angle KDC=\alpha $$, то накрест лежащие углы при секущей $$ MD$$ равны $$ \alpha $$; это по теореме означало бы параллельность прямых $$ MB$$ и $$ CB$$, что противоречит их пересечению. Этот случай невозможен.
б) Если $$ \angle KDC=2\alpha $$, то по теореме о сумме углов треугольника (для треугольника $$ KDC$$) $$ \alpha +2\alpha +2\alpha =180°$$ ,$$ \alpha =36°$$. Находим углы треугольника $$ ABC$$ :$$ \angle A=\angle C=2\alpha =72°$$ , $$ \angle B=180°-2·\angle A=36°$$.
III. Для прямоугольных треугольников справедливы признаки равенства (их надо уметь доказывать):
1. по двум катетам;
2. по гипотенузе и катету;
3. по гипотенузе и острому углу;
4. по катету и острому углу.
Применяя признаки равенства прямоугольных треугольников, докажем ещё один признак равнобедренного треугольника:
Доказать, что если две высоты треугольника равны, то он равнобедренный.
Решение
Пусть высоты $$ A{A}_{1}$$ и $$ C{C}_{1}$$ треугольника $$ ABC$$ равны друг другу.
1. (Треугольник остроугольный. Обе высоты внутри треугольника, (рис. 12а). Прямоугольные треугольники $$ A{A}_{1}B$$ и $$ C{C}_{1}B$$ равны по катету ($$ A{A}_{1}=C{C}_{1}$$) и противолежащему острому углу (угол $$ B$$ – общий). Тогда
равны их гипотенузы $$ AB=CB$$, а это и означает, что треугольник $$ ABC$$ равнобедренный.
| Рис. 12a | Рис. 12б |
Рис. 12в |
2. (Треугольник тупоугольник, угол $$ В$$ тупой. Обе высоты вне треугольника, рис. 12б). Прямоугольные треугольники $$ A{A}_{1}B$$ и $$ C{C}_{1}B$$ имеют равные катеты $$ A{A}_{1}=C{C}_{1}$$ и равные противолежащие углы $$ \angle AB{A}_{1}=\angle CB{C}_{1}$$ как вертикальные . Треугольники равны, равны их гипотенузы $$ AB=CB$$. Треугольник $$ ABC$$ – равнобедренный.
3. Случай равенства двух высот равнобедренного треугольника, одна из которых внутри треугольника, другая – вне треугольника, невозможен. Действительно, если $$ B{B}_{1}=A{A}_{1}=h$$ (рис. 12в), то $$ △A{A}_{1}B=△B{B}_{1}A$$ по гипотенузе (у них общая $$ AB$$) и катету $$ A{A}_{1}=B{B}_{1}$$. Тогда $$ \angle BA{A}_{1}=\angle AB{B}_{1}$$ (обозначен $$ \alpha $$ ), т. е. накрест лежащие углы при секущей $$ AB$$ равны и прямые $$ A{A}_{1}$$ и $$ {B}_{1}B$$ параллельны, что неверно.
4. Если угол $$ B$$ – прямой, то высоты из вершин $$ A$$ и $$ C$$ совпадают с катетами $$ AB$$ и $$ CB$$.
При равных высотах равны и катеты, треугольник $$ ABC$$ – равнобедренный.
Доказать, что медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Решение
| Рис. 13 |
Точка $$ M$$ – середина гипотенузы $$ AB$$ прямоугольного треугольника $$ ABC$$ (рис. 13). Проведём через точку $$ M$$ прямую $$ MK\perp AC$$.
Из $$ BC\perp AC$$ и $$ MK\perp AC$$ следует $$ BC\parallel MK$$.
Из параллельности прямых $$ BC$$ и $$ MK$$ и равенства отрезков $$ BM$$ и $$ MA$$ по теореме Фалеса следует $$ CK=KA$$.
В прямоугольных треугольниках $$ CMK$$ и $$ AMK$$ катет $$ MK$$ общий и, как установили, равны катеты $$ CK$$ и $$ AK$$. Эти треугольники равны, значит, равны и их гипотенузы, т. е. $$ CM=AM$$, или $$ CM={\displaystyle \frac{1}{2}}AB$$.
Дополнение. Для многих учащихся при решении задач возникает проблема: с чего начать? С рисунка! В геометрической задаче очень важен рисунок, он должен отвечать условиям задачи, быть наглядной формой их записи.
| Рис. 14a | Рис. 14б |
Например, в задаче рассматривается равнобедренный треугольник. Его можно нарисовать по-разному (рис. 14а и 14б), поэтому сначала рисуют на черновике, от руки, и из других условий определяют вид треугольника.
Если сказано, что один отрезок в два раза длиннее другого, – отразите это на рисунке; если какие-то прямые параллельны – так и рисуйте, т. е. после таких рассмотрений делаете чёткий хороший рисунок, отвечающий условиям задачи.
Хороший рисунок – помощник в решении, особенно если на нём Вы отмечаете равные углы, перпендикулярность отрезков, отношение длин и т. п. и ставите данные задачи. Посмотрите, например, на рис. 7, 8, 11 и подумайте, как рисунок помогает в решении.
В треугольнике $$ ABC$$ медиана $$ BM$$ перпендикулярна биссектрисе $$ AD$$. Найти длину стороны $$ AB$$, если $$ AC=6$$.
Решение
△ 1. Подумаем, как построить рисунок. Возьмём луч $$ AK$$ (рис. 15) и отложим от точки $$ A$$ какие-то равные углы (т. е. считаем, что биссектриса $$ AD$$ лежит на этом луче).
| Рис. 15 |
Выберем точку $$ B$$, проведём через точку $$ B$$ прямую, перпендикулярно $$ AK$$ и отметим точку $$ M$$, $$ BM$$ – медиана, поэтому отложим отрезок $$ MC=MA$$. Треугольник $$ ABC$$ – тот, что нужен: $$ AD$$ – биссектриса, $$ BM$$ – медиана, $$ AD\perp BM$$.
2. Решение очевидно: $$ △ABO=△AMO$$ (по катету и острому углу), значит $$ AB=AM$$ и $$ AC=2AM=2AB$$. Зная, что $$ AC=6$$, находим $$ AB=3$$.

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны (рис. 16). Параллелограмм – выпуклый четырёхугольник. В разных учебниках различные определения выпуклого четырёхугольника, приведём два равносильных определения:
1) Четырёхугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону.
2) Четырёхугольник называется выпуклым, если его диагонали пересекаются.
Равносильность доказывается на основе свойства полуплоскостей.
Легко доказывается теорема, что сумма углов выпуклого четырёхугольника равна `360^@` (повторите по учебнику).
Рис. 16
Свойства параллелограмма
Признаки параллелограмма
Докажем, например, признак 3.
Пусть в четырёхугольнике `ABCD` стороны удовлетворяют условиям `AB=DC` и `BC=AD` (рис. 17). Отметим соответственно равные стороны и проведём диагональ `AC`. `Delta ABC= Delta CDA` (`AB=CD`, `BC=AD`, `AC` - общая сторона). В равных треугольниках против равных сторон лежат равные углы: против `AB` - угол `1`, против `CD` - угол `2`, `/_ 1 = /_ 2` (накрест лежащие углы) . Против `BC` - угол `3`, против `AD` - угол `4`, `/_ 3 = /_ 4 =>` .
Противолежащие стороны попарно параллельны, значит параллелограмм по определению.
Свойства параллелограмма используются для доказательства замечательной теоремы о высотах треугольника.
Три высоты или три прямые, на которых лежат высоты треугольника, пересекаются в одной точке.
Через каждую вершину треугольника `ABC` (рис. 18) проведём прямую, параллельную противолежащей вершине стороне. Получаем треугольник `A_1 B_1 C_1`, к сторонам которого перпендикулярны высоты данного (например, если `AH _|_ BC`, то из , следует `AH_|_B_1 C_1`).
По построению , , - параллелограмм. Также показывается, что `AC_1BC` - параллелограмм. По свойству параллелограмма `BA_1 = AC`, `C_1 B = AC => C_1 B = BA_1`, т. е. точка `B` - середина стороны `A_1 C_1`. Повторяя рассуждение, устанавливаем, что точка `A` - середина стороны `B_1 C_1` и точка `C` - середина стороны `A_1 B_1`.
Прямые, на которых лежат высоты `AH`, `BF` и `CK` треугольника `ABC`, перпендикулярны к сторонам треугольника `A_1 B_1 C_1` и проходят через их середины, а три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке (определяют центр окружности, описанной около треугольника `A_1 B_1 C_1`). Значит три прямые, на которых лежат высоты, пересекаются в одной точке.
Если треугольник остроугольный, то пересекаются сами высоты.
Если в треугольнике `ABC` углы `A` и `C` - острые (рис. 19), то вершина `B` лежит в полосе между двумя параллельными прямыми `l_1` и `l_2`, которые проходят через точки `A` и `C` и перпендикулярны `AC`. Отсюда следует, что основание `F` её высоты `BF` лежит на стороне `AC`. Если угол `B` - также острый (т. е. треугольник `ABC` - остроугольный), то основание `H` высоты `AH` тоже лежит на стороне `BC` (рассуждения те же самые). Точки `B` и `F` лежат в разных полуплоскостях, образованных прямой `AH`, значит отрезок `BF` пересекает прямую `AH`. Точка пересечения `O` лежит на `BF`, т. е. лежит внутри треугольника, и, значит, на отрезке `AH`. По теореме третья высота пройдёт через ту же точку `O`.
Биссектриса угла `A` параллелограмма `ABCD` пересекает сторону `CD` в точке `K`, а продолжение стороны `BC` в точке `F` (рис. 20). Найти стороны параллелограмма, если `BF = 16` и `CK =5`.
`AF` - биссектриса угла `BAD`, . Прямые `AD` и `BF` - параллельны, поэтому (как накрест лежащие), тогда `/_2 = /_3`, треугольник `ABF` -равнобедренный, `AB=BF`. Значит `AB =16`.
По свойству параллелограмма `CD=AB`, значит `CD=16` и `DK=11`. Далее, из следует `/_2 = /_4` (накрест лежащие), значит `/_4=/_1`, треугольник `ADK` - равнобедренный, `AD=DK=11`.
`AD=BC=11`, `AB=CD=16`.
Дана окружность с диаметром `AB` и точка `M`, лежащая внутри окружности, но не на диаметре (рис. 21). С помощью односторонней линейки опустить из точки `M` перпендикуляр на прямую `AB`.
( – уменьшенная копия односторонней линейки).
Что мы можем делать с помощью односторонней линейки? Проводить прямые! Вот и проведём через точки `A` и `M` прямую до пересечения с окружностью в точке `A_1`, затем через точки `B` и `M` проведём прямую до пересечения с окружностью в точке `B_1` (рис. 21).
Далее, проведём прямую через точки `A` и `B_1` и прямую через точки `B` и `A_1` - получим в их пересечении точку `C`. Прямая `CM` - искомая. В треугольнике `ACB` высоты `A A_1` и `B B_1` (углы `A A_1 C` и `B B_1 C` - прямые, опираются на диаметр) пересекаются в точке `M`. Точка `M` - точка пересечение высот треугольника `ACB`, значит `C C_1 _|_ AB`.
Если точка `M` лежит вне окружности и не на прямой `AB`, решение задачи усложняется, но немного (попробуйте сами).
Параллелограмм, в котором все углы прямые, называется прямоугольником.
Верна теорема: диагонали прямоугольника равны.
Верна и обратная теорема - признак прямоугольника: если диагонали параллелограмма равны, то этот параллелограмм - прямоугольник.
Параллелограмм, у которого все стороны равны, называется ромбом. Сформулируйте сами две теоремы о диагоналях ромба и обратные к ним.
Прямоугольник, у которого все стороны равны, называется квадратом. Квадрат - правильный четырёхугольник.
Через середину диагонали `BD` прямоугольника `ABCD` проведена перпендикулярно этой диагонали прямая, пересекающая сторону `BC` в точке `F` и сторону `AD` в точке `E`. Известно, что `EF = ED = 8`. Найти большую сторону прямоугольника.
Середина диагонали `BD` - точка `O`, - есть центр прямоугольника, `BO=OD` (рис. 22). Отрезок `EF` делится точкой `O` пополам, действительно, `Delta BOF = Delta DOE` (углы при точке `O` равны как вертикальные, `/_DBF = /_BDE` (как накрест лежащие при параллельных прямых `BC` и `AD`) и `BO=OD`; треугольники равны по второму признаку равенства).
Значит `FO=EO=1/2 EF=4` и `BF=ED=8`.
Треугольник `BOF` - прямоугольный, гипотенуза `BF=8`, катет `OF=4`, значит `/_OBF =30^@`.
Диагонали прямоугольника равны, равны и их половины, `BO=OC`. Треугольник `BOC` - равнобедренный, `/_BCO=30^@`, `/_CFO=180^@ - /_OFB =180^@ - 60^@ = 120^@`,
следовательно `/_FOC = 30^@`. Треугольник `OFC` - равнобедренный, `FC=OF=4`, значит `BC=12`.
`12`.
Окружность, построенная как на диаметре, на стороне `AD` параллелограмма `ABCD` касается стороны `BC` и проходит через середину стороны `AB` (рис. 23). Найти углы параллелограмма.
Пусть `O` - центр окружности и `R` - её радиус. Если `P` - точка касания стороны `BC`, то `OP_|_ BC`, а из следует `OP_|_AD`. Это означает, что расстояние между параллельными прямыми `AD` и `BC` равно `R`.
Точка `M` лежит на окружности, `OM=R`. Точка `M` - середина стороны `AB`. Если `MF _|_ AD` и `MK _|_ BC`, то точки `K`, `M` и `F` лежат на одной прямой (т. к. ) и поэтому `KF=PO=R`. Прямоугольные треугольники `AMF` и `BMK` равны (по гипотенузе и острому углу) и `MF=1/2 KF = 1/2 R`.
Из треугольника `OMF`, в котором `MF_|_OF`, `OM=R` и `MF= R/2` следует, что `/_MOF = 30^@`.
Далее заметим, что треугольник `AOM` равнобедренный `(OA=OM=R)`,
угол при вершине `O` равен `30^@`, следовательно `/_OAM = /_ AMO = 75^@`.
Итак, острый угол `A` параллелограмма равен `75^@`, а тупой угол `B` равен `105^@`.
`75^@` и `105^@`.

1. Как измерить с помощью одной мерной линейки, произведя одно измерение, диагональ кирпича (крпич имеет форму прямоугольного параллелепипеда, изображённого на рис. 24, его диагональ - это отрезок, соединяющий проивоположные вершины (например, `A` и `B`)). Дайте способ простой, практичный, пригодный для мастерской, стройки, без приминения вычислений по теореме Пифагора.
2. Тяжёлая балка `AB` лежит на брёвнах (рис. 25), её правый конец отстоит от оси последнего бревна на `5` м (`BC=5` м). На сколько продвинется вперёд передняя часть балки (точка `A`), если точка `B` достигент оси последнего бравна? Считать брёвна одинаоковыми и круглыми; катятся брёвна без скольжения.
3. Нетрудно показать, что у правильно пятиугольной звезды сумма углов равна `180^@`. Показать, что такая же сумма углов будет у произвольной пятиугольной звезды (рис. 26).
4. Во времена частных междоусобных войн один правитель захотел построить крепость-замок из `10` башен, соединённых между собой стенами, причём стены должны тянуться прямыми линиями с четырьмя башнями в каждой из них. Приглашённый им известный строитель представил ему план крепости (см. рис. 27), но правитель нашёл его совершенно неудовлетворительным: при таком расположении к любой из десяти башен можно подойти извне. Правителю же хотелось, чтобы по крайней мере одна башня (а ещё лучше - две) была бы со всех сторон защищена стеной от вторжения извне. Долго строитель ломал голову над такой задачей, но решил её и с одной безопасной башней, и с двумя безопасными башнями.
Попробуйте и вы найти решение.
5. Можно ли покрыть костяшками домино (каждая костяшка – две клетки) доску `8` x `8` клеток с двумя вырезанными противоположными клетками (рис. 28)?
6. Три одинаковых треугольника разрезали по медианам (рис. 29). Сложите из полученных `6` кусков один треугольник.
7. На рис. 30 изображена фигура, составленная из пяти квадратов. Требуется провести два разреза по прямым линиям так, чтобы из полученных частей можно было бы составить квадрат.
8. Найти площадь треугольника, изображённого на клетчатой бумаге (см. рис. 31), считать площадь каждой клетки равной `1`.
9. На окружности расположено `2000` чёрных точек и одна белая точка. Рассматриваются всевозможные выпуклые многоугольники с вершинами в этих точках. Каких многоугольников больше: тех, у которых все вершины чёрные, или тех, у которых одна вершина белая?
10. Можно ли, начав движение в какой-то точке контура обойти все его звенья, проходя по каждому ровно `1` раз, и вернуться в исходную точку? (контуры `1`-`6` на рис. 32)
11. Какое наибольшее число острых углов может иметь выпуклый `n` - угольник?

В контрольных вопросах и задачах проверяются Ваши знания основного курса и знакомство с материалом нашего задания.
1. Контрольные вопросы и задачи могут быть не только по темам, повторенным в этом Задании (повторить весь учебник невозможно), но и по материалу, изученному Вами в школе. При ответе на некоторые вопросы придётся открыть учебник.
2. Ответы на контрольные вопросы надо давать обоснованные. Приведём примеры.
Точки `K` и `L` делят диагональ `AC` параллелограмма `ABCD` на три равные части: `AK=KL=LC` (рис. 33). Верно ли, что прямые `BK` и `LD` параллельны?
Да, верно. Докажем это.
а) Проведём диагональ `BD`. По теореме диагонали параллелограмма пересекаются и точкой пересечения делятся пополам: `AO=OC` и `BO=OD`.
б) Из `AO = OC` и `AK=CL` следует `KO=OL`.
в) `Delta BOK = Delta DOL`, так как `KO=OL`, `BO=OD` и `/_BOK = /_ DOL` (как вертикальные).
Из равенства треугольников следует `/_ 1 = /_ 2`. Накрест лежащие углы при секущей `AC` равны, следовательно, .
В четырёхугольнике `ABCD` стороны `AB` и `CD` равны друг другу, а стороны `AD` и `BC` параллельны. Является ли четырёхугольник `ABCD` параллелограммом?
Нет, например, четырёхугольник `ABCD` на рисунке 34 удовлетворяет этим условиям, но противоположные стороны `AB` и `CD` не параллельны (этот четырёхугольник - равнобокая трапеция).

Вспомним некоторые понятия и определения, изученные вами в восьмом классе.
Число $$ a$$ называется решением (или корнем) уравнения, если при его подстановке в уравнение вместо неизвестной уравнение превращается в верное равенство. Решить уравнение – значит найти все его корни или доказать, что корней нет.
Точно так же определяется понятие решения неравенства, а именно: число $$ a$$ называется решением неравенства, если при подстановке числа $$ a$$ вместо переменной в неравенство получается верное неравенство. Решить неравенство – значит найти все его решения или доказать, что их нет.
Совокупность всех решений уравнения (неравенства) называют множеством решений уравнения (неравенства). Если уравнение (неравенство) не имеет решений, то говорят, что его множество решений пусто (обозначается значком $$ \varnothing $$).
Уравнения (неравенства) называются равносильными, если множества их решений совпадают. Заметим также, что уравнение и неравенство могут быть равносильны друг другу. (Обозначение: (1) $$ \iff $$ (2)).
Среди следующих пар уравнений и неравенств выберите равносильные:
а) $$ \left|x\right|=2$$ и $$ {x}^{4}-{x}^{2}-12=0$$;
б) $$ \sqrt{x-12}=24-x$$ и $$ x-12=(24-x{)}^{2}$$;
в) $$ {x}^{2}\le x$$ и $$ x\le 1$$;
г) $$ x\ge 0$$ и $$ \left|x\right|=x$$;
д) и $$ {x}^{2}+3x+3=0$$.
a) По определению модуля $$ \left|x\right|=2\iff $$ $$ \left[\begin{array}{l}x=2,\\ x=-2.\end{array}\right.$$
Решим уравнение $$ {x}^{4}-{x}^{2}-12=0$$. Сделаем замену $$ {x}^{2}=t$$. Тогда получаем $$ {t}^{2}-t-12=0$$, откуда $$ \left[\begin{array}{l}t=4,\\ t=-3.\end{array}\right.$$
Поэтому $$ {x}^{4}-{x}^{2}-12=0\iff $$ $$ \left[\begin{array}{l}{x}^{2}=4,\\ {x}^{2}=-3\end{array}\right.$$ $$ \iff {x}^{2}=4\iff $$ $$ \left[\begin{array}{l}x=2,\\ x=-2.\end{array}\right.$$
Значит, уравнения равносильны.
б) $$ x-12=(24-x{)}^{2}\iff x-12={x}^{2}-48x+576\iff $$
$$ \iff {x}^{2}-49x+588=0\iff \left[\begin{array}{c}x=21,\\ x=28.\end{array}\right.$$
Заметим, что $$ x=28$$ не является решением первого уравнения (при подстановке $$ x=28$$ получаем неверное равенство $$ 4=-4$$), поэтому уравнения не равносильны.
в) Чисо $$ x=-1$$ является решением второго неравенства, но не является решением первого. Значит, их множества решений не совпадают, и неравенства равносильными не являются.
г) По определению модуля, уравнению $$ \left|x\right|=x$$ удовлетворяет любое $$ x\ge 0$$. Отрицательных решений это уравнение не имеет, т. к. при левая часть положительна, а правая - отрицательна. Получаем, что данные уравнение и неравенство равносильны.
д) И уравнение, и неравенство не имеют решений, поэтому они равносильны.
При решении уравнений можно действовать двумя способами.
1) Все выполняемые преобразования равносильны. Тогда мы сразу получаем ответ.
2) Если мы делаем какие-то неравносильные преобразования, то ни одно из них не должно приводить к потере корней. (Действительно, если корень потерялся, то его никак не вернёшь). Значит, нам можно делать только такие неравносильные преобразования, в результате которых мы можем приобрести лишние корни. В таком случае в конце решения необходимо сделать отбор корней: подставляя все найденные значения переменной в исходное уравнение, отбираем те из них, которые являются его корнями. Естественно, этот способ не проходит, если уравнение имеет бесконечно много решений (так как при отборе корней нельзя подставить бесконечное количество значений в уравнение). Тогда приходится делать только равносильные преобразования.
Некоторые преобразования всегда приводят нас к равносильным уравнениям, например, перенесение слагаемых из одной части уравнения в другую, умножение обеих частей уравнения на отличное от нуля число и др. Применяя другие преобразования (приведение подобных слагаемых, сокращение дробей, возведение обеих частей уравнения в квадрат и пр.), мы иногда получаем равносильные уравнения, а иногда нет. Когда мы решаем неравенства, почти всегда отбор корней сделать невозможно (так как неравенства обычно имеют бесконечно много реше-ний), поэтому необходимо делать только равносильные преобразования.
Рассмотрим два уравнения
$$ {f}_{1}\left(x\right)={g}_{1}\left(x\right)$$ (1)
$$ {f}_{2}\left(x\right)={g}_{2}\left(x\right)$$ (2)
Говорят, что уравнение (2) является следствием уравнения (1) (пишут (1)$$ \Rightarrow $$(2)), если каждый из корней уравнения (1) является также и корнем уравнения (2). Иначе говоря, множество решений уравнения (1) содержится в множестве решений уравнения (2).
Несложно видеть, что если из (1) следует (2), а из (2) следует (1), то уравнения (1) и (2) равносильны.
Например, $$ x=2\Rightarrow (x-2)(x-3)=0$$; $$ {x}^{2}+1=0\Rightarrow x=5$$ (действительно, множество решений первого уравнения пусто, а пустое множество является подмножеством любого множества). Таким образом, если уравнение (неравенство) не имеет корней, то из него следует любое другое уравнение (неравенство).

Квадратным называют уравнение
$$ a{x}^{2}+bx+c=0$$, (3)
где $$ a\ne 0$$.
Если разделить обе части уравнения (3) на $$ a$$ (это можно сделать, так как $$ a\ne 0$$) и обозначить коэффициенты $$ p=b/a$$ и $$ q=c/a$$, то получим уравнение
$$ {x}^{2}+px+q=0$$ (4)
называемое приведённым квадратным уравнением.
Левую часть в (3) и (4) называют квадратным трёхчленом. Корни уравнения называют также корнями трёхчлена.
Все вы, конечно же, знаете формулу корней квадратного уравнения. Ввиду особой важности метода выделения полного квадрата, напомним способ её получения. Преобразуем левую часть (3):
$$ a{x}^{2}+bx+c=a\left({x}^{2}+\frac{b}{a}x+\frac{c}{a}\right) =a\left({x}^{2}+2·\frac{b}{2a}·x+\frac{c}{a}\right)=$$
$$ =a\left({x}^{2}+2·\frac{b}{2a}x+{\left(\frac{b}{2a}\right)}^{2}-{\left(\frac{b}{2a}\right)}^{2}+\frac{c}{a}\right)=a\left({\left(x+\frac{b}{2a}\right)}^{2}-\frac{{b}^{2}-4ac}{4{a}^{2}}\right)$$. (5)
Выражение $$ {b}^{2}-4ac$$ называется дискриминантом и обозначается буквой $$ D$$. С учётом этого обозначения уравнение (3) можно переписать в виде:
$$ {\left(x+{\displaystyle \frac{b}{2a}}\right)}^{2}={\displaystyle \frac{D}{4{a}^{2}}}$$ (6)
Из (6) при $$ D\ge 0$$ получаем $$ {x}_{1}=-{\displaystyle \frac{b}{2a}}+{\displaystyle \frac{\sqrt{D}}{2a}}$$; $$ {x}_{2}=-{\displaystyle \frac{b}{2a}}-{\displaystyle \frac{\sqrt{D}}{2a}}$$.
Эти формулы можно объединить одной записью
$$ {x}_{\mathrm{1,2}}={\displaystyle \frac{-b\pm \sqrt{D}}{2a}}$$ (7)
Обратим внимание, что при $$ D=0$$ выходит, что $$ {x}_{1}={x}_{2}$$. В этом случае говорят, что квадратное уравнение имеет один корень кратности `2`.
Если в уравнении (3) коэффициент $$ b$$ имеет вид $$ b=2k$$ (например, если $$ b$$ - чётное число), то удобнее использовать формулы, получаемые из (7) сокращением на `2` числителя и знаменателя:
| $$ {x}_{\mathrm{1,2}}={\displaystyle \frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}}={\displaystyle \frac{-2k\pm \sqrt{4{k}^{2}-4ac}}{2a}}={\displaystyle \frac{-k\pm \sqrt{{k}^{2}-ac}}{a}}$$ |
`(7^')` |
Например, корни уравнения $$ 81{x}^{2}-42x+5=0$$ проще найти по формулам (7'), чем (7). Здесь $$ b=-42=2(-21)$$, поэтому
$$ {x}_{\mathrm{1,2}}={\displaystyle \frac{21\pm \sqrt{{21}^{2}-81·5}}{81}}={\displaystyle \frac{21\pm \sqrt{9({7}^{2}-9·5)}}{81}}= {\displaystyle \frac{21\pm 3\sqrt{4}}{81}}={\displaystyle \frac{7\pm 2}{27}}$$,
$$ {x}_{1}={\displaystyle \frac{5}{27}}, {x}_{2}={\displaystyle \frac{1}{3}}$$.
Если дискриминант квадратного трёхчлена неотрицателен, то выкладки (5) можно продолжить:
`a((x+ b/(2a))^2 - D/(4a^2) ) = a((x+ b/(2a) )^2 - ((sqrtD)/(2a))^2)=a(x+b/(2a) - (sqrtD)/(2a))(x+b/(2a) + (sqrtD)/(2a))=`
`=a(x-(-b+sqrtD)/(2a))(x-(-b-sqrtD)/(2a))=a(x-x_1)(x-x_2)`.
Таким образом, если квадратный трёхчлен $$ a{x}^{2}+bx+c$$ имеет корни, то он раскладывается на множители $$ a{x}^{2}+bx+c=a(x-{x}_{1})(x-{x}_{2})$$. В случае $$ D=0$$ корни совпадают `(x_1 = x_2 = x_0)`, и тогда получаем $$ a{x}^{2}+bx+c=a(x-{x}_{0}{)}^{2}$$.
Заметим, что квадратный трёхчлен $$ a{x}^{2}+bx+c$$ имеет корни, то `x_1 + x_2 = (- b + sqrtD)/(2a) + (- b - sqrtD)/(2a) = - b/a`;
`x_1 * x_2 = (-b+ sqrtD)/(2a) * (-b-sqrtD)/(2a) = (b^2 - D)/(4a^2) = (b^2 - (b^2 - 4ac))/(4a^2) = c/a`.
Полученный результат называют теоремой Виета. Для приведённого квадратного трёхчлена $$ {x}^{2}+px+q$$ теорема Виета выглядит так: если есть корни `x_1` и `x_2`, то `x_1 + x_2 = - p`, `x_1 x_2 =q`.
Имеет место и теорема, обратная теореме Виета:
если числа $$ {x}_{1}$$ и $$ {x}_{2}$$ удоветворяют условиям $$ {x}_{1}+{x}_{2}=p$$, $$ {x}_{1}·{x}_{2}=q$$, то эти числа являются корнями уравнения $$ {x}^{2}-px+q=0$$.
Доказательство этой теоремы - это один из контрольных вопросов Задания. Иногда для краткости обе теоремы Виета (прямую и обратную) называют просто теорема Виета.
Решите уравнение:
a) $$ {x}^{2}+(\sqrt{3}+\sqrt{17})x+\sqrt{51}=0$$;
б) $$ 2016{x}^{2}+2017x+1=0$$;
в) $$ \sqrt{3}{x}^{2}+(5-2\sqrt{3})x+(\sqrt{3}-5)=0$$.
a) По теореме, обатной теореме Виета, $$ {x}_{1}=-\sqrt{3}$$ и $$ {x}_{2}=-\sqrt{17}$$ - корни данного уравнения.
$$ x=-\sqrt{3};x=-\sqrt{17}$$.
б) Заметим, что $$ {x}_{1}=-1$$ является корнем данного уравнения. Значит, уравнение имеет корни, и по теореме Виета, их произведение $$ {x}_{1} · {x}_{2} = {\displaystyle \frac{1}{2016}}$$, откуда $$ {x}_{2 }= {\displaystyle \frac{-1}{2016}}$$.
$$ x=-1;x={\displaystyle \frac{-1}{2016}}$$.
в) Заметим, что $$ {x}_{1}=1$$ является корнем (это легко видеть, т. к. сумма всех коэффициентов в уравнении равна нулю). Из условия $$ {x}_{1}·{x}_{2}={\displaystyle \frac{\sqrt{3}-5}{\sqrt{3}}}$$ получаем, что $$ {x}_{2}=1-{\displaystyle \frac{5}{\sqrt{3}}}$$.
$$ x=1;x=1-{\displaystyle \frac{5}{\sqrt{3}}}$$.
Найти наибольшее значение выражения $$ 4+7x-3{x}^{2}$$.
Будем осуществлять методом выделения полного квадрата.
$$ 4+7x-3{x}^{2}=-3\left({x}^{2}-{\displaystyle \frac{7}{3}}x\right)+4=-3\left({x}^{2}-2·{\displaystyle \frac{7}{6}}x +{\displaystyle \frac{49}{36}}-{\displaystyle \frac{49}{36}}\right)+4=$$ $$ -3\left({\left(x-{\displaystyle \frac{7}{6}}\right)}^{2}-{\displaystyle \frac{49}{36}}\right)+4=-3{\left(x-{\displaystyle \frac{7}{6}}\right)}^{2}+{\displaystyle \frac{49}{12}} +4=-3{\left(x-{\displaystyle \frac{7}{6}}\right)}^{2}+{\displaystyle \frac{97}{12}}$$.
$$ -3{\left(x-{\displaystyle \frac{7}{6}}\right)}^{2}\le 0$$ при всех $$ x$$, поэтому максимальное значение выражения достигается, если $$ -3{\left(x-{\displaystyle \frac{7}{6}}\right)}^{2}=0$$. Значит, это максимальное значение равно $$ {\displaystyle \frac{97}{12}}$$ (достигается при $$ x={\displaystyle \frac{7}{6}}$$).
$$ {\displaystyle \frac{97}{12}}$$.
Пусть $$ {x}_{1}$$ и $$ {x}_{2}$$ - корни квадратного уравнения $$ a{x}^{2}+bx+c=0$$. выразите $$ {x}_{1}^{2}+{x}_{2}^{2}$$ через коэффициенты уравнения.
По теореме Виета $$ {x}_{1}+{x}_{2}=-{\displaystyle \frac{b}{a}},{x}_{1}{x}_{2}={\displaystyle \frac{c}{a}}$$. Преобразуем $$ {x}_{1}^{2}+{x}_{2}^{2}$$, выделяя полный квадрат:
$$ {x}_{1}^{2}+{x}_{2}^{2}={x}_{1}^{2}+{x}_{2}^{2}+2{x}_{1}·{x}_{2}-2{x}_{1}·{x}_{2}=({x}_{1}+{x}_{2}{)}^{2}-2{x}_{1}·{x}_{2}$$.
Отсюда: $$ {x}_{1}^{2}+{x}_{2}^{2}={\left(-{\displaystyle \frac{b}{a}}\right)}^{2}-2{\displaystyle \frac{c}{a}}={\displaystyle \frac{{b}^{2}-2ac}{{a}^{2}}}$$.
$$ {\displaystyle \frac{{b}^{2}-2ac}{{a}^{2}}}$$.

Многочленом с одной переменной называется выражение вида
`P(x) = a_n x^n + a_(n-1) x^(n-1) +a_(n-2) x^(n-2) + ... + a_2 x^2 + a_1 x + a_0 (a_n != 0)`. (8)
Числа `a_0`, `a_1`, `...`, `a_n` - это коэффициенты многочлена; `a_n` называют старшим коэффициентом, `a_0` - свободным членом.
Степенью многочлена называют наибольшую степень переменной, входящую в многочлен.
Например, степень многочлена `P = x^4 - x^3 - x^2 + 2x + 1` равна `4`; степень многочлена `25 + x^5 - 3x` равна `5`; степень многочлена `17` равна `0`, т. к. переменная в это выражение не входит; наконец, выражение `3x^2 + x +5+ 2/x` многочленом не является, поэтому о его степени говорить бессмысленно. Многочлен `P(x) = 0` называют нулевым многочленом. Степень нулевого многочлена не определена.
Два многочлена называются равными, если равны все их коэффициенты. Многочлен равен нулю, если все его коэффициенты равны нулю.
Число `a` называется корнем многочлена `F(x)`, если `F(alpha) = 0`.
Приведём основные сведения о многочленах.
Для любых двух многочленов `F(x)` и `G(x)` существует единственная пара многочленов `P(x)` (частное) и `Q(x)` (остаток) такая, что `F(x) = G(x) * P(x) + Q(x)`, причём степень остатка `Q(x)` меньше степени делителя `G(x)`, или `Q(x)` есть нулевой многочлен. Покажем, как на практике находят частное и остаток от деления многочленов.
Разделите с остатком многочлен `F(x) = 18x^5 + 27x^4 -37x^3 - 14x + 20`
на многочлен `G(x) = 2x^2 + 3x -5`.
Процедура деления многочленов очень похожа на деление целых чисел. Если степень делимого не меньше степени делителя, то делаем следующее: делим старший член многочлена `F(x)` на старший член многочлена `G(x)`, получившийся результат записываем в частное. Умножаем результат на весь делитель `G(x)` и вычитаем полученное из исходного многочлена `F(x)`. После этих действий член со старшей степенью `x` сокращается. Если в результате вычитания у оставшегося многочлена степень не меньше, чем степень делителя, то можно сделать ещё один шаг деления и т. д.
Деление закончится тогда, когда степень делимого будет меньше степени делителя. В случае, когда в делимом отсутствуют некоторые степени переменных, для удобства записи лучше оставить пустые места для соответствующих членов (хотя это не обязательно).
Вернёмся к нашему примеру. Первый член частного равен `(18x^5)/(2x^2) = 9x^3`. При умножении на делитель `2x^2 +3x-5` получаем `18x^5 + 27x^4 - 45x^3`. После вычитания из исходного многочлена от него остаётся `8x^3 -14x +20`. Степень многочлена, оставшегося после вычитания, равна `3`. Это больше степени делителя, поэтому можно сделать следующий шаг деления. Делим `8x^3` на `2x^2` и получаем `4x`, умножаем `4x` на `2x^2 +3x-5`, получаем `8x^3 +12x^2 -20`; вычитаем этот многочлен из `8x^3 -14x +20` и т. д.
Частное равно `9x^3 +4x -6`; остаток равен `24x-10`.
Таким образом, `18x^5 + 27x^4 - 37x^3 -14x + 20 = (2x^2 + 3x - 5)(9x^3 + 4x - 6) + (24x - 10)`.
Теорема 2. (Теорема Безу и следствия из неё).
1) Теорема Безу. Остаток от деления многочлена `F(x)` на многочлен `(x-alpha)` равен `F(alpha)`.
2) Число `alpha` является корнем многочлена `F(x)` тогда и только тогда, когда многочлен `F(x)` делится на многочлен `(x-alpha)`.
3) Если `alpha` и `beta` - различные корни многочлена `F(x)`, то он делится на многочлен `(x- alpha)(x- beta)`.
4) Многочлен степени `n` не может иметь более `n` корней.
1) Разделим с остатком многочлен `F(x)` на многочлен `(x-alpha)`. Тогда остаток либо равен нулю, либо является многочленом нулевой степени (т. к. степень остатка меньше степени делителя, а степень делителя равна `1`). Поэтому можно записать, что
`F(x) = (x-alpha) G(x) +C` (9)
Через `G(x)` здесь обозначено частное от деления, вид которого нас не интересует.
Равенство (9) верно при всех значениях `x`. Подставим в него `x=alpha`.
Тогда `F(alpha) = (alpha - alpha)G(alpha) + C`, или `F(alpha) = C`.
Подставим `C=F(alpha)` в (9) и получим
`F(x) = (x - alpha) G (x) + F(alpha)`. (10)
Первая часть доказана.
2) Из (10) следует, что `F(x)` делится на `(x - alpha)` тогда и только тогда, когда `F(alpha) = 0`, т. е. тогда и только тогда, когда `alpha` есть корень многочлена `F(x)`.
3) `alpha` - корень `F(x) => F(x)` делится на `(x- alpha) => F(x) = (x- alpha) G(x)`. Подставим в последнее равенство (которое верно для всех значений переменной `x`) `x= beta`. Тогда `F(beta) = (beta - alpha) G(beta)`.
`F(beta) = 0` (т. к. `beta` -корень `F(x)`), поэтому `(beta - alpha)G(beta) = 0 =>G(beta) = 0` (т. к. `beta != alpha`); отсюда `G(x)` делится на `(x- beta)`, т. е. `G(x) = H(x) * (x- beta)`. Подведём итог: `F(x) = (x- alpha) G(x) = (x -alpha)(x- beta) H(x)`, т. е. `F(x)` делится на `(x- alpha)(x- beta)`.
4) Теперь становится понятным, что многочлен степени `n` не может иметь больше, чем `n` корней.
Остатки от деления многочлена `F(x)` на многочлены `(x-3)` и `(x+5)` равны `2` и `(-9)` соответственно. Найдите остаток от деления многочлена `F(x)` на многочлен `x^2 + 2x -15`.
Заметим, что `x^2 + 2x -15 = (x-3)(x+5)`.
По теореме Безу `F(3) = 2`; `F(-5) =-9`.
Поделим `F(x)` с остатком на `x^2 + 2x -15`:
`F(x) = (x^2 + 2x - 15)G(x) + r(x)`.
Степень остатка не превосходит степени делителя, поэтому остаток – это либо многочлен первой степени, либо нулевой степени, либо равен нулю. В любом случае, остаток представим в виде `r(x) = ax +b` (если `a!= 0`, то получим многочлен первой степени; если `a=0`, `b!=0`, то будет многочлен нулевой степени; если `a=b=0`, то получим нулевой многочлен). Итак,
`F(x) = (x^2 + 2x-15)G(x) + ax+b`. (11)
Подставим в равенство (11) `x=3` и `x=-5`:
`F(3) = 0 * G(3) + 3a + b`; `F(-5)=0 * G(-5) -5a+b`, откуда $$ \left\{\begin{array}{l}3a+b=2,\\ -5a+b=-9.\end{array}\right.$$
Решая эту систему, нахоим, что `a=(11)/8`, `b=- (17)/8`.
Докажите, что
$$ \sqrt[3]{26-15\sqrt{3}}+\sqrt[3]{26+15\sqrt{3}}=4$$. (12)
Пусть $$ \sqrt[3]{26-15\sqrt{3}}+\sqrt[3]{26+15\sqrt{3}}=x$$. Возведём обе части этого равенства в куб и преобразуем:
$$ 26-15\sqrt{3}+3\sqrt[3]{{\left(26-15\sqrt{3}\right)}^{2}}\sqrt[3]{26+15\sqrt{3}}+3\sqrt[3]{26-15\sqrt{3}}\sqrt[3]{{\left(26+15\sqrt{3}\right)}^{2}}+26+15\sqrt{3}={x}^{3}$$;
$$ 52+3\sqrt[3]{26-15\sqrt{3}}\sqrt[3]{26+15\sqrt{3}}\left(\sqrt[3]{26-15\sqrt{3}}+\sqrt[3]{26+15\sqrt{3}}\right)={x}^{3}$$;
$$ 52+3\sqrt[3]{{26}^{2}-{\left(15\sqrt{3}\right)}^{2}}\left(\sqrt[3]{26-15\sqrt{3}}+\sqrt[3]{26+15\sqrt{3}}\right)={x}^{3}$$;
$$ 52+3\left(\sqrt[3]{26-15\sqrt{3}}+\sqrt[3]{26+15\sqrt{3}}\right)={x}^{3}$$;
`52+3x=x^3`;
`x^3-3x-52=0`. (13)
Число `x=4` является корнем этого уравнения. Докажем, что других корней нет (и тем самым будет доказана справедливость равенства (12)). Поскольку `x=4` является корнем, многочлен `x^3 - 3x-52` делится на `x-4` без остатка. Выполняя деление, получаем:
$$ {x}^{3}-3x-52=0\iff \left(x-4\right)\left({x}^{2}+4x+13\right)=0\iff \left[\begin{array}{l}x-4=0,\\ {x}^{2}+4x+13=0.\end{array}\right.$$
У квадратного трёхчлена `x^2 +4x+13` отрицательный дискриминант, поэтому уравнение (13) имеет ровно один корень `x=4`.
При каких `a` и `b` многочлен `F(x)=x^4 +ax^3 - 2x^2 +19x+b` делится на многочлен `x^2 -3x+2`?
1-й способ. Выполним деление с остатком:
Приравниваем коэффициенты остатка к нулю
$$ \left\{\begin{array}{l}7a+28=0,\\ b-6a-10=0,\end{array}\right.\iff \left\{\begin{array}{l}a=-4,\\ b=-14.\end{array}\right.$$
2-й способ. `x^2 -3x+2=(x-1)(x-2)`.
Многочлен делится на `(x-1)(x-2)` тогда и только тогда, когда `x=1` и `x=2` являются корнями многочлена. То есть,
$$ \begin{array}{c}F\left(1\right)=1+a-2+19+b=0, \\ F\left(2\right)=16+8a-8+38+b=0,\end{array}\iff \left\{\begin{array}{l}18+a+b=0,\\ 46+8a+b=0,\end{array}\right.\iff \left\{\begin{array}{l}a=-4,\\ b=-14.\end{array}\right.\phantom{\rule{0ex}{0ex}}$$
`a=-4`, `b=-14`.

Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени? Оказывается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 - 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
$$ \iff \left[\begin{array}{l}x-1=0,\\ {x}^{2}+5x+3=0,\end{array}\right.\iff \left[\begin{array}{l}x=1,\\ x={\displaystyle \frac{-5\pm \sqrt{13}}{2}}.\end{array}\right.$$
`x=1`; `x=(-5+- sqrt13)/2`.
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравнения? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` - целое, `q` - натуральное) является корнем многочлена с целыми коэффициентами, то свободный член делится на `p`, а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` - корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ ...``+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + ... + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
`p(a_np^(n-1)+a_(n-1)p^(n-2)q+a_(n-2)p^(n-3)q^2+...+a_2pq^(n-2)+a_1q^(n-1))=-a_0q^n`. (14)
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
Решите уравнение
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` - корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
`539=7^2*11`.
Поэтому `p` может принимать значения:
`+-1,+-7,+-11,+-49,+-77,+-539`.
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
`(x+1)(x^3+3x^2-105x-539)=0`.
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
`(x+1)(x+7)(x+7)(x-11)=0`.
`x=-7`; `x=-1`; `x=11`.
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in{+-1;+-2;+-5;+-10}`; `qin{1;2;3;6}`.Возможные варианты для `x_0`:
`+-1,+-2,+-5,+-10,+-1/2,+-5/2,+-1/3,+-2/3,+-5/3,+-10/3,+-1/6,``+-5/6`.
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
`(2x-5)(3x^2-10x^2-11x-2)=0`.
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` - корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
`(2x-5)(3x+2)(x^2-4x-1)=0`.
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
`x=5/2`; `x=-2/3`; `x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4`;
б)* `x^3-3x^2-3x-1`;
в) `x^4-x^3+2x^2-2x+4`;
г)* `x^4-4x^3-20x^2+13x-2`.
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
`=(x^2+2-2x)(x^2+2+2x)`.
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
`a^4+b^4=(a^2+b^2)^2-2a^2b^2=`
`=(a^2-sqrt2ab+b^2)(a^2+sqrt2ab+b^2)`.
б)* `x^3-3x^2-3x-1=2x^3-(x^3+3x^2+3x+1)`$$ ={\left(\sqrt[3]{2}x\right)}^{3}-{\left(x+1\right)}^{3}=$$
$$ =\left(\sqrt[3]{2}x-x-1\right)\left(\sqrt[3]{4}{x}^{2}+\sqrt[3]{2}x\left(x+1\right)+{\left(x+1\right)}^{2}\right)$$.
в) Вынесем `x^2` за скобки и сгруппируем:
`x^4-x^3+2x^2-2x+4=x^2(x^2-x+2-2/x+4/x^2)=``x^2((x^2+4/x^2)-(x+2/x)+2)`.
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
`t^2-4-t+2=t^2-t-2=(t+1)(t-2)=(x+2/x+1)(x+2/x-2)`.
В итоге получаем:
`x^2(x+2/x+1)(x+2/x-2)=(x^2+2+x)(x^2+2-2x)=(x^2+x+2)(x^2-2x+2)`.
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
`x^2(x^2-2/x^2_(4x-13/x)-20)`.
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
`x^4-4x^3-20x^2+13x-2=(x^2+ax+b)(x^2+cx+d)`. (17)
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
`x^4-4x^3-20x^2+13x-2=`
`=x^4+(a+c)x^3+(b+ac+d)x^2+(ad+bc)x+bd`. (18)
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
$$ \left\{\begin{array}{l}a+c=-4,\\ b+ac+d=-20,\\ ad+bc=13,\\ bd=-2.\end{array}\right.$$ (19)
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
1) `b=1` и `d=-2`;
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
1) $$ \left\{\begin{array}{l}a+c=-4,\\ ac=-19,\\ -2a+c=13.\end{array}\right.$$
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
2) $$ \left\{\begin{array}{l}a+c=-4,\\ ac=-21,\\ -a+2c=13.\end{array}\right.$$
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
`x^4-4x^3-20+13x-2=(x^2-7x+2)(x^2+3x-1)`.
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
Решите уравнение:
а) `(x-4)^2+|x-4|-2=0`;
б) `(x-7)^4+(x+1)^4=706`;
в) `1/(x^2+2x-3)+18/(x^2+2x+2)=18/((x+1)^2)`;
г) `(x-2)(x-4)(x+5)(x+7)=360`;
д) `(4x)/(4x^2-8x+7)+(3x)/(4x^2-10x+7)=1`;
е) `25x^4-150x^3+94x^2+150x+25=0`.
а) Обозначим `|x-4|=t`. Тогда `(x-4)^2=t^2` и получаем `t^2+t-2=0`, откуда $$ \left[\begin{array}{l}t=1,\\ t=-2.\end{array}\right.$$
Если `t=-2`, то решений нет.
Если `t=1`, то `|x-4|=1 iff`$$ \left[\begin{array}{l}x=3,\\ x=5.\end{array}\right.$$
`x=3`; `x=5`.
б) Обозначим `x-3=t`. Тогда получим
`(t-4)^4+(t+4)^4=706 iff(t^4-16t^3+96t^2-256t+256)+`
`+(t^4+16t^3+96t^2+256+256)=706 iff2t^4+192t^2-194=0iff`
`ifft^4+96t^2-97=0 iff(t^2-1)(t^2+97)=0 ifft=+-1`.
Значит, `x_1=4`, `x_2=2`.
`x=2`, `x=4`.
Уравнения вида `(x-a)^4+(x-b)^4=c` с помощью замены `x-((a+b))/2=t` сводятся к биквадратным.
в) Обозначим `x^2+2x+1=t`. Тогда `1/(t-4)+18/(t+1)=18/tiff`
$$ \iff \left\{\begin{array}{l}{t}^{2}+t+18\left({t}^{2}-4t\right)=18\left({t}^{2}-3t-4\right)\\ t\left(t+1\right)\left(t-4\right)\ne 0\end{array}\right.\iff $$
$$ \iff \left\{\begin{array}{l}{t}^{2}-17t+72=0,\\ t\left(t+1\right)\left(t-4\right)\ne 0\end{array}\right.\iff \left[\begin{array}{l}t=8,\\ t=9.\end{array}\right.$$
Теперь найдём `x:`
$$ \left[\begin{array}{l}{\left(x+1\right)}^{2}=8,\\ {\left(x+1\right)}^{2}=9\end{array}\right.\iff \left[\begin{array}{l}x+1=\pm 2\sqrt{2},\\ x+1=\pm 3\end{array}\right.\iff $$
$$ \iff \left[\begin{array}{l}x=-1-2\sqrt{2},\\ x=-1+2\sqrt{2},\\ x=2,\\ x=-4.\end{array}\right.$$
`x=-1+-2sqrt2`; `x=2`; `x=-4`.
г) Перемножим первую скобку с третьей, а вторую с четвёртой (убедитесь сами, что только такая группировка сомножителей помогает свести уравнение к квадратному).
`((x-2)(x+5))*((x-4)(x+7))=360iff`
`iff(x^2+3x-10)(x^2+3x-28)=360`.
Обозначим `x^2+3x-19=t`. Тогда уравнение принимает вид:
`(t+9)(t-9)=360ifft^2=441ifft=+-21`,
откуда
$$ \left[\begin{array}{l}{x}^{2}+3x-19=21,\\ {x}^{2}+3x-19=-21\end{array}\right.\iff \left[\begin{array}{l}{x}^{2}+3x-40=0,\\ {x}^{2}+3x+2=0\end{array}\right.\iff \left[\begin{array}{l}x=5,\\ x=-8,\\ x=-1,\\ x=-2.\end{array}\right.$$
`x=-8`; `x=-2`; `x=-1`; `x=5`.
д) Разделим числитель и знаменатель каждой дроби на `x` (`x=0` не является решением уравнения):
`4/(4x-8+7/x)+3/(4x-10+7/x)=1`. Обозначим `4x+7/x-8=t`. Тогда
$$ {\displaystyle \frac{4}{t}}+{\displaystyle \frac{3}{t-2}}=1\iff \left\{\begin{array}{l}4\left(t-2\right)+3t={t}^{2}-2t,\\ t\left(t-2\right)\ne 0\end{array}\right.\iff $$
$$ \iff \left\{\begin{array}{l}{t}^{2}-9t+8=0,\\ t\left(t-2\right)\ne 0\end{array}\right.\iff \left[\begin{array}{l}t=1,\\ t=8.\end{array}\right.$$
Теперь найдём `x:` $$ \left[\begin{array}{l}4x+{\displaystyle \frac{7}{x}}-8=1,\\ 4x+{\displaystyle \frac{7}{x}}-8=8\end{array}\right.\iff \left[\begin{array}{l}4{x}^{2}-9x+7=0,\\ 4{x}^{2}-16x+7=0.\end{array}\right.$$
Уравнение `4x^2-9x+7=0` не имеет решений, а у уравнения `4x^2-16x+7=0` корнями являются числа `x=7/2` и `x=1/2`.
`x=1/2`; `x=7/2`.
е) `x!=0` (убеждаемся подстановкой), поэтому при делении обеих частей уравнения на `x^2` получим уравнение, равносильное исходному:
`25x^2-150x+94+150*1/x+25*1/x^2=0iff`
`iff(25x^2+25*1/x^2)-(150x-150*1/x)+94=0iff`
`iff25(x^2+1/x^2)-150(x-1/x)+94=0`.
Обозначим `x-1/x=t`. Тогда `t^2=(x-1/x)^2=x^2-2+1/x^2`, откуда `x^2+1/x^2=t^2+2`. Подставляем и решаем уравнение относительно `t:`
`25(t^2+2)-150t+94=0iff25t^2-150t+144=0iff5t^2-30t+144/5=0`.
Коэффициент при `t` чётный; по формуле четверти дискриминанта:
`D/4=15^2-5*(144)/5=225-144=81`; `t_1=(15+9)/5=24/5`; `t_2+(15-9)/5=6/5`.
Теперь найдём `x:`
$$ \left[\begin{array}{l}x-{\displaystyle \frac{1}{x}}={\displaystyle \frac{24}{5}},\\ x-{\displaystyle \frac{1}{x}}={\displaystyle \frac{6}{5}}\end{array}\right.\iff \left[\begin{array}{l}5{x}^{2}-24x-5=0,\\ 5{x}^{2}-6x-5=0\end{array}\right.\iff \left[\begin{array}{l}x=-{\displaystyle \frac{1}{5}};\\ x=5;\\ x={\displaystyle \frac{3\pm \sqrt{34}}{5}}.\end{array}\right.$$
`5`; `-1/5`; `(3+-sqrt(34))/5`.
1) Уравнения вида `ax^4+bx^3+cx^2+bx+a=0` называются возвратными. Для их решения делят обе части уравнения на `x^2` и вводят замену `x+-1/x=t`.
2) Некоторые другие уравнения четвёртой степени решаются с помощью замены `ax+b/x=t`. (См. пример 11в).

В каждом параграфе сгруппированы теоремы, которые в учебнике рассыпаны по разным главам. Здесь мы компактно напоминаем теорию, приводим примеры решения характерных задач, доказываем некоторые дополнительные утверждения, показываем определённые приёмы решений.
Прежде чем приступать к выполнению домашнего задания, рекомендуем проработать предложенный материал «с карандашом», параграф за параграфом: вспомнить одни и узнать другие теоремы, выписать и выучить формулы, прорешать приведённые примеры.
Контрольные вопросы составлены так, чтобы проверить, как Вы усвоили темы Задания, есть ли пробелы в знаниях, умеете ли Вы решать несложные задачи на доказательство, делать выводы из разобранных теорем, а также видеть «подводные камни» в вопросах и задачах.
Приступая к ответам на контрольные вопросы, сделайте рисунок (если надо) на черновике, уясните вопрос, подберите нужный пример или продумайте доказательство. Окончательные ответы должны быть достаточно подробные. В случае отрицательного ответа должен быть приведён опровергающий пример. Примеры ответов приведены в конце задания.
Задачи могут Вам показаться сложнее решаемых в школе. Если задача не получается, найдите в тексте подобную ей задачу и разберите её решение. Либо подумайте, на какую тему – и повторите соответствующий параграф, а затем сделайте ещё одну попытку.
Может случиться, что не все задачи удалось решить. Печально, но не следует приходить в отчаяние. Ведь и не предполагается, что все поступившие в ЗФТШ уже все знают и умеют. Школа как раз и хочет научить Вас, поэтому высылайте то, что получилось. Обратно Вы получите проверенную Вашу тетрадь и, кроме того, подробные решения всех задач и ответы на все вопросы. Это даст Вам возможность разобрать «не поддавшиеся» задачи, узнать, как они решаются, и в другой раз, в следующем задании, в работе в школе, на олимпиаде, выступить успешнее.
Каждый ответ и решение каждой задачи оцениваются в очках. За полное правильное решение или верный ответ выставляется то число очков, которое указано в скобках после номера вопроса или задачи. За ошибки, недочёты снимается некоторое число очков. За неверный ответ на вопрос или неправильное решение задачи ставится ноль очков.
В решениях и доказательствах иногда делаем по 2 - 3 рисунка для того, чтобы легче было следить за ходом рассуждений.

Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`c` - гипотенуза `AB`;
`a` и `b` – катеты `BC` и `AC` (по-гречески "kathetos - катет" означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
Напомним, что если `alpha` - величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то
`sin alpha = a/c`, `cos alpha = b/c` и `"tg"alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
`a^2 = c * a_c`
`b^2 = c * b_c`
Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ - alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.
Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c`. Аналогично доказывается второе равенство.
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
`h^2 = a_c * b_c`
Из треугольника `ACD` (рис. 1) имеем `"tg"alpha = (CD)/(AD)`, а из треугольника `BCD` `"tg"alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
`a * b = c * h`
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
`m_c = 1/2 c`
Пусть `AM = BM`. Проведём $$ MK\Vert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`
.
Кроме того, из того, что `BC _|_ AC` и $$ MK\Vert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
`R = m_c = 1/2 c`
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Пусть `O` - центр вписанной окружности и `F`, `N` и `S` - точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` - квадрат со стороной `r`, поэтому `BF = BC - FC`, `AN = AC - CN`, т. е. `BF = a - r` и `AN = b - r`.
Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` - общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b - r`.
Аналогично доказывается, что `BS = a - r`, поэтому из `AB = AS + BS` следует `c = (b - r) + (a - r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.
Высота, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Приведём примеры применения доказанных метрических соотношений в прямоугольном треугольнике.
Проекции катетов прямоугольного треугольника на гипотенузу равны `9` и `16` . Найти радиус вписанной окружности.
1. Пусть `a_c = 9`, `b_c = 16` (рис. 4), тогда `c = a_c + b_c = 25`.
2. По Свойству 1: `a = sqrt(c * a_c) = 15`, `b = sqrt(c * b_c) = 20`.
3. По Свойству 6: находим радиус `r = 1/2 (a + b - c) = 5`.
В прямоугольном треугольнике из вершины прямого угла проведены медиана и высота (рис. 5), расстояние между их основаниями равно `1`. Найти катеты, если известно, что один из них в два раза больше другого.
1. Заметим, что `a_c = c/2 - 1`, a `b_c = c/2 + 1` (рис. 5), откуда `a^2 = c * a_c = c(c/2 - 1)` и `b^2 = c * b_c = c(c/2 + 1)`.
2. По условию `b = 2a`, значит `b^2 = 4a^2`, т. е. `c(c/2 + 1) = 4c(c/2 - 1)`.
Находим `c = (10)/3`, и `a = sqrt(c(c/2 - 1)) = 2/3 sqrt5` и `b = 2a = 4/3 sqrt5`.

Первые две теоремы Вам хорошо известны, две другие – докажем.
Три биссектрисы треугольника пересекаются в одной точке, которая есть центр вписанной окружности.
основано на том факте, что биссектриса угла есть геометрическое место точек, равноудалённых от сторон угла.
Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, которая есть центр описанной окружности.
основано на том, что серединный перпендикуляр отрезка есть геометрическое место точек, равноудалённых от концов этого отрезка.
Три высоты или три прямые, на которых лежат высоты треугольника, пересекаются в одной точке. Эта точка называется ортоцентром треугольника.
Через вершины треугольника `ABC` проведём прямые, параллельные противолежащим сторонам (рис. 6).
В пересечении образуется треугольник `A_1 B_1 C_1`.
По построению `ABA_1C` - параллелограмм, поэтому `BA_1 = AC`. Аналогично устанавливается, что `C_1B = AC`, следовательно `C_1B = AC`, точка `B` - середина отрезка `C_1A_1`.
Совершенно так же показывается, что `C` - середина `B_1A_1` и `A` - середина `B_1 C_1`.
Пусть `BN` - высота треугольника `ABC`, тогда для отрезка `A_1 C_1` прямая `BN` - серединный перпендикуляр. Откуда следует, что три прямые, на которых лежат высоты треугольника `ABC`, являются серединными перпендикулярами трёх сторон треугольника `A_1B_1C_1`; а такие перпендикуляры пересекаются в одной точке (теорема 2).
Если треугольник остроугольный, то каждая из высот есть отрезок, соединяющий вершину и некоторую точку противолежащей стороны. В этом случае (см. рис. 6) точки `B` и `N` лежат в разных полуплоскостях, образуемых прямой `AM`, значит отрезок `BN` , пересекает прямую `AM`, точка пересечения лежит на высоте `BN`, т. е. лежит внутри треугольника.
В прямоугольном треугольнике точка пересечения высот есть вершина прямого угла.
Три медианы треугольника пересекаются в одной точке и каждая медиана делится точкой пересечении в отношении `2:1`, считая от вершины. Эта точка называется центром тяжести (или центром масс) треугольника.
Есть различные доказательства этой теоремы. Приведём то, которое основано на теореме Фалеса.
Пусть `E`, `D` и `F` - середины сторон `AB`, `BC` и `AC` треугольника `ABC` (рис. 7а).
Проведём медиану `AD` и через точки `E` и `F` параллельные ей прямые `EK` и `FL`. По теореме Фалеса `BK = KD` `(/_ABC`, $$ EK\Vert AD)$$ и `DL = LC` `(/_ACB`, $$ AD\Vert FL)$$. Но `BD = DC = a//2`, поэтому `BK = KD = DL = LC = a//4`. По тойже теореме `BN = NM = MF` `(/_ FBC`, $$ NK\Vert MD\Vert FL)$$, поэтому `BM = 2MF`.
Это означает, что медиана `BF` в точке `M` пересечения с медианой `AD` разделились в отношении `2:1` считая от вершины.
Докажем, что и медиана `AD` в точке `M` разделилась в том же отношении. Рассуждения аналогичны, иллюстрация на рисунке 7б.
Если рассмотреть медианы `BF` и `CE` то также можно показать, что они пересекаются в той точке, в которой медиана `BF` делится в отношении `2:1` т. е. в той же точке `M`. И этой точкой медиана `CE` также разделится в отношении `2:1`, считая от вершины.
Две стороны треугольника равны соответственно `6` и `8`. Медианы, проведённые к этим сторонам, пересекаются под прямым углом. Найти третью сторону треугольника.
1. Пусть `AC = 6`, `BC = 8` и медианы `AN` и `BM` пересекаются в точке `O` и перпендикулярны (рис. 8).
Положим `AN = n` и `BM = m`. Из доказанной теоремы следует, что `AO = 2/3 n` и `BO = 2/3 m`.
2. Медианы перпендикулярны, поэтому треугольники `AOM` и `BON` прямоугольные.
Применим теорему Пифагора (ещё учтём, что `AM = 1/2 AC = 3` и `BN = 1/2 BC = 4`),
получим: $$
\left\{
\begin{aligned}
16=\frac49 m^2+\frac19 n^2,\\
9=\frac19 m^2 + \frac49 n^2.\\
\end{aligned}
\right.
$$
Сложив эти равенства, найдём, что `m^2 + n^2 = 45`.
3. Длина стороны `AB` находится из прямоугольного треугольника `AOB:`
`x^2 = 4/9m^2 + 4/9n^2 = 4/9(m^2 + n^2) = 20`.
Итак, `AB = 2 sqrt5`.
Свойства высот и биссектрис будут далее рассмотрены в §3.

Две фигуры `F` и `F'` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F'` подобны, то пишется `F ~ F'`. Напомним, что запись подобия треугольников `Delta ABC ~ Delta A_1 B_1 C_1` означает, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. `A` переходит в `A_1`, `B` - в `B_1`, `C` - в `C_1`.
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC ~ Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,
`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.
Два треугольника подобны, если:
1. два угла одного соответственно равны двум углам другого;
2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
3. три стороны одного треугольника пропорциональны трём сторонам другого.
В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.
Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.
Доказательство
Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.
И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.
Решение
1. Пусть `O` - точка пересечения диагоналей, `AD = a`, `BC = b`. Прямая `MN` параллельна основанию `AD` (рис. 10а), следовательно, $$ MO\parallel AD$$, треугольники `BMO` и `BAD` подобны, поэтому
`(MO)/(AD) = (BO)/(BD)` (1)
2. $$ AD\parallel BC$$, `Delta AOD ~ Delta COB` по двум углам (рис. 10б):
`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.
3. Учитывая, что `BD = BO + OD` находим отношение
`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.
Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.
Точки `M` и `N` лежат на боковых сторонах `AB` и `CD` трапеции `ABCD` и $$ MN\parallel AD$$ (рис. 11а). Найти длину `MN`, если `BC = a`, `AD = 5a`, `AM : MB = 1:3`.
1. Пусть $$ BF\Vert CD$$ и $$ ME\Vert CD$$ (рис. 11б), тогда `/_ 1 = /_ 2`, `/_ 3 = /_ 4` (как соответствующие углы при пересечении двух параллельных прямых третьей) и `Delta AME ~ Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.
2. Обозначим `MN = x`. По построению `BCNF` и `MNDE` - параллелограммы, `FN = a`, `ED = x` и, значит, `MF = x - a`; `AE = 5a - x`. Итак, имеем `(5a - x)/(x - a) = 1/3`, откуда находим `x = 4a`.
Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.
Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.
Попытайтесь доказать это самостоятельно.
Прямоугольные треугольники подобны, если:
1. они имеют по равному острому углу;
2. катеты одного треугольника пропорциональны катетам другого;
3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.
Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.
Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.
СВОЙСТВА ВЫСОТ И БИССЕКТРИС
Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` - его высоты, то `Delta A_1B_1C ~ Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).
Доказательство
Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).
В треугольнике `A A_1C` угол `A_1` - прямой, `A_1C = AC cos C = ul (b cos C)`.
В треугольнике `B B_1C` угол `B_1` - прямой, `B_1C = BC cos C = ul (a cos C)`.
В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.
Таким образом, `Delta A_1 B_1 C ~ Delta ABC` с коэффициентом подобия `ul (cos C)`. (Заметим, что `/_ A_1 B_1 C = /_B`).
б) Треугольник `ABC` - тупоугольный (рис. 12б), угол `C` - острый, высота `A A_1` проведена из вершины тупого угла.
Рассуждения аналогичны:
$$\left.\begin{array}{rcl}
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos C =b \cos C;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos C =a \cos C,
\end{array}
\right\}\Rightarrow \Delta A_1B_1C\sim \Delta ABC,$$
коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.
Случай, когда угол `B` тупой, рассматривается аналогично.
в) Треугольник `ABC` - тупоугольный (рис. 12в), угол `C` - тупой, высоты `A A_1` и `B B_1` проведены из вершин острых углов.
`varphi = /_ BCB_1 = /_ ACA_1 = 180^@ - /_ C`, `cos varphi = - cos C = |cos C|`.
$$\left.\begin{array}{rcl}
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos\varphi =b |\cos C|;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos\varphi =b |\cos C|,
\end{array}
\right\}\Rightarrow \Delta A_1B_1C\sim \Delta ABC$$
с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.
В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).
Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).
Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).
Решение
По первой лемме о высотах `Delta A_1 B_1 C ~ Delta ABC`, `/_ A_1 B_1 C = /_ B`.
Аналогично `Delta AB_1C_1 ~ Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.
Так как `BB_1` - высота, то `/_AB_1B = /_CB_1B = 90^@`.
Поэтому `/_C_1B_1B = /_A_1B_1B = 90^@ - /_B`, т. е. луч `B_1B` - биссектриса угла `A_1B_1C_1`.
Аналогично доказывается, что `A A_1` - биссектриса угла `B_1 A_1 C_1` и `C_1C` - биссектриса угла `B_1 C_1 A_1`.
Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.
Решение
`Delta AHB_1 ~ Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.
Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.
Решение
1. По условию пересекаются высоты, поэтому треугольник остроугольный. Положим `BH = HB_1 = x` и `HA_1 = y`, тогда `AH = 2y`. По второй лемме о высотах `AH * HA_1 = BH * HB_1`, т. е. `x^2 = 2y^2`, `x = y sqrt 2`.
2. В треугольнике `AHB_1` угол `AHB_1` равен углу `C` (т. к. угол `A_1 AC` равен `90^@ - C`), поэтому `cos C = cos (/_ AHB_1) = x/(2y) = sqrt 2/ 2`. Угол `C` - острый, `/_ C = 45^@`.
Ответ:
`/_ C = 45^@`.
Установим ещё одно свойство биссектрисы угла треугольника.
Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если `AD` - биссектриса треугольника `ABC`, то `(BD)/(DC) = (AB)/(AC)`.
Доказательство
Проведём через точку `B` прямую параллельно биссектрисе `DA`, пусть `K` - её точка пересечения с прямой `AC` (рис. 16).
Параллельные прямые `AD` и `KB` пересечены прямой `KC`, образуются равные углы `1` и `3`. Те же прямые пересечены и прямой `AB`, здесь равные накрест лежащие углы `2` и `4`. Но `AD` - биссектриса, `/_1 = /_2`, следовательно `/_3 = /_4`. Отсюда следует, что треугольник `KAB` равнобедренный, `KA = AB`.
По теореме о пересечении сторон угла параллельными прямыми из $$ AD\Vert KB$$ следует `(BD)/(DC) = (KA)/(AC)`. Подставляя сюда вместо `KA` равный ему отрезок `AB`, получим `(BD)/(DC) = (AB)/(AC)`. Теорема доказана.
Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.
Решение
Пусть `AD` - биссектриса и `BD = 3`, `DC = 5` (рис. 17).
По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x < 3x + 8)`, `3x < 5x + 8` и `ul (8 < 3x + 5x)`. Получаем ограничения `x<4` и `x > 1`.
Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16 < P < 40)`.

Рассмотрим задачи, решения которых основаны на теореме о пресечении угла параллельными прямыми и подобии треугольников. Напомним теорему:
Параллельные прямые, пересекая стороны угла, отсекают на них пропорциональные отрезки, т. е. если $$ {l}_{1}\parallel {l}_{2}$$, то `(AC)/(AB) = (AC_1)/(AB_1) = (C C_1)/(BB_1)` или `m/x = (m + n)/(x + y) = n/y`.
Точка `N` лежит на стороне `AC` треугольника `ABC` причём `AN:NC = 2:3`. Найти, в каком отношении медиана `AM` делит отрезок `BN`.
1. Пусть `O` - точка пересечения медианы `AM` и отрезка `BN`. Требуется найти отношение `BO:ON`. Обозначим `AN = 2x`, тогда `NC = 3x`. Отметим, что `BM = MC` (рис. 18а).
Проведём прямую `NK` параллельно медиане `AM` (рис. 18б).
Параллельные прямые `AM` и `NK` пересекают стороны угла `MCA`, следовательно, `(MK)/(KC) = 2/3`. Полагаем `ul (MK = 2y)`, тогда `KC = 3y`, а т. к. `BM = MC`, то `ul (BM = 5y)`.
2. Те же прямые пересекают стороны угла `NBC` (см. рис. 18в), поэтому `(BO)/(ON) = (BM)/(MK) = (5y)/(2y)`, т. е. `(BO)/(ON) = 5/2`.
Точки `D` и `F` лежат на сторонах `AB` и `BC` треугольника `ABC` (рис. 19), при этом `AD:DB = 1:2` и `BF:FC = 2:3`. Прямая `DF` пересекает прямую `AC` в точке `K`. Найти отношение `AK:AC`.
1. Пусть `AD = x`, `BF = 2y`, `KA = z`. Тогда `DB = 2x` и `FC = 3y`.
Проводим прямую `AE`, параллельную стороне `CB`.
`Delta ADE ~ Delta BDF| => AE:BF = AD:BD => ul(AE = y)`.
2. `Delta KAE ~ Delta KCF | => (KA)/(KC) = (AE)/(CF)`, т. е. `z/(a + z) = y/(3y)`. Находим `a = 2z`.
`AK:AC = 1:2`.
В треугольнике `ABC` точки `D` и `K` лежат соответственно на сторонах `AB` и `AC`, отрезки `BK` и `CD` пересекаются в точке `O` (рис. 20), при этом `BO:OK = 3:2` и `CO:OD = 2:1`. Найти в каком отношении точка `K` делит сторону `AC`, т. е. `AK:KC`.
1. Полагаем `OD = x`, `OK = 2y`, тогда `OC = 2x` и `BO = 3y`.
Проводим прямую $$ KF\parallel CD$$ (рис. 20б).
Из $$ KF\parallel OD$$ `(/_ ABK)` следует `BD:DF = 3:2`. Обозначаем `DF = 2p`, тогда `BD = 3p`.
2. `Delta FBK ~ Delta DBO`, `FK:DO = FB:DB`, откуда `FK = (5p)/(3p) * x = 5/3 x`.
3. `Delta AFK ~ Delta ADC`, `AF:AD = FK:DC`. Обозначаем `AF = z`, имеем `z/(z + 2p) = (5/3 x)/(3x)`,
откуда `z = 5/2 p`, т. е. `AF = 5/2 p`.
4. Рассматриваем `/_ BAC`, $$ FK\parallel DC$$, по теореме `AK:KC = AF:FP`, т. е. `AK:KC = 5:4`.
Все три рассмотренные задачи могут быть решены с применением теоремы Менелая.
Пусть в треугольнике `ABC` точка `A_1` лежит на стороне `BC`, точка `C_1` - на стороне `AB`, а точка `B_1` - на продолжении стороны `AC` за точку `C`.
Если точки `A_1`, `B_1` и `C_1` лежат на одной прямой (рис. 21), то выполняется равенство
`(AC_1)/(C_1 B) * (BA_1)/(A_1C) * (CB_1)/(B_1A) = 1`. `(**)`
Обратно, если выполняется равенство `(**)`, то точки `A_1`, `B_1` и `C_1` лежат на одной прямой. (Заметим, что можно считать `B_1C_1` секущей треугольника `ABC`, а можно считать `BC` секущей треугольника `AB_1C_1`).
а) Предположим, что точки `A_1`, `B_1` и `C_1` лежат на одной прямой. Проведём $$ CK\parallel AB$$ (рис. 21). `Delta CKB_1 ~ Delta AC_1B_1`, поэтому `(CK)/(AC_1) = (CB_1)/(AB_1)`, откуда `CK = (CB_1)/(AB_1) * AC_1`.
Далее: `Delta CKA_1 ~ Delta BC_1A_1`, значит
`(CK)/(BC_1) = (CA_1)/(BA_1)`.
Подставляя сюда выражение для `CK`, получим `(CB_1)/(AB_1) * (AC_1)/(BC_1) = (CA_1)/(BA_1)`, т. е. `(AC_1)/(C_1B) * (BA_1)/(A_1C) * (CB_1)/(B_1A) = 1`, ч. т. д.
б) Пусть выполнено равенство `(**)` для точек `A_1`, `B_1` и `C_1` (рис. 22), докажем, что эти точки лежат на одной прямой.
Через две точки `A_1` и `B_1` проведём прямую, пусть `C_2` - её точка пересечения с прямой `AB` (точка пересечения будет лежать на отрезке `AB`).
Три точки `A_1`, `B_1` и `C_2` лежат на одной прямой и по доказанному в пункте а) выполняется равенство
`(AC_2)/(C_2B) * (BA_1)/(A_1C) * (CB_1)/(B_1A) = 1`.
Сравнив это равенство с равенством `(**)`, придём к выводу, что `(AC_2)/(C_2B) = (AC_1)/(C_1B)`. Точки `C_2` и `C_1` лежат на отрезке `AB` и делят его в одном отношении, считая от конца `A`. Следовательно, точка `C_2` совпадает с точкой `C_1`, т. е. точки `A_1`, `B_1` и `C_1` лежат на одной прямой.
Стрелки на рисунке 21 (от точки `A`) показывают, как легко запомнить последовательность отрезков в пропорции `(**)`.
Например, применим теорему Менелая к задаче из примера 12. Полагаем `BO = m`, `ON = n` (см. рис. 23) и рассматриваем треугольник `CBN` и секущую `AM`.
Имеем:
`(CM)/(BM) * (BO)/(ON) * (NA)/(AC) = 1`, т. е. `1/1 * m/n * (2x)/(5x) = 1`, откуда `m/n = 5/2`.