 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы

Конденсатором называется система, состоящая из двух проводников, расположенных достаточно близко друг от друга. Проводники называют обкладками конденсатора. Если на обкладки конденсатора поместить равные по модулю и противоположные по знаку заряды, то разность потенциалов (напряжение) между обкладками будет пропорциональна заряду обкладок, т. е. отношение заряда к напряжению не будет зависеть от заряда. На основании этого утверждения, которое приводим без доказательства, вводится понятие электроёмкости (ёмкости конденсатора).
Ёмкостью конденсатора называется отношение заряда $$ Q$$ одной из обкладок к разности потенциалов $$ U$$ между этой обкладкой и соседней:
| $$ C={\displaystyle \frac{Q}{U}}$$. | (10.1) |
Если взят заряд на положительно заряженной обкладке, то $$ Q>0, U>0$$ и получится $$ C>0$$. Если заряд взят на отрицательной обкладке, то и опять будет $$ C>0$$. Итак, из определения ёмкости следует, что ёмкость величина положительная. В системе СИ ёмкость измеряется в фарадах: `1"Ф"=1` Кл/В.
Требование близости обкладок друг к другу связано с тем, что для независимости $$ C$$ от $$ Q$$ в (10.1) нужно, чтобы поле от зарядов на обкладках было сосредоточено практически полностью между обкладками, т. е. все силовые линии, начинающиеся на одной обкладке, заканчивались только на другой и не уходили на окружающие тела. В этом случае окружающие тела не будут влиять на ёмкость конденсатора.
Можно вывести, что ёмкость плоского конденсатора
| $$ C={\displaystyle \frac{\varepsilon {\varepsilon }_{0}S}{d}}$$. | (10.2) |
Здесь $$ S$$ - площадь обкладок, $$ d$$ - расстояние между ними, $$ \varepsilon $$ - диэлектрическая проницаемость диэлектрика между обкладками.
При последовательном соединении изначально не заряженных конденсаторов с ёмкостями $$ {C}_{1}, {C}_{2}, ...$$, общий заряд равен заряду каждого конденсатора, общее напряжение равно сумме напряжений на отдельных конденсаторах, общая ёмкость определяется из формулы: $$ {\displaystyle \frac{1}{C}}={\displaystyle \frac{1}{{C}_{1}}}+{\displaystyle \frac{1}{{C}_{2}}}+...$$
Полезно помнить формулу для частного случая последовательного соединения двух конденсаторов: $$ C={\displaystyle \frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}}$$.
Для последовательно соединённых n одинаковых конденсаторов ёмкостью $$ {C}_{1}$$ каждый $$ C={C}_{1}/n.$$
Если последовательно соединены предварительно заряженные конденсаторы, то применение перечисленных выше свойств и формул может привести к неправильному результату!
При параллельном соединении конденсаторов с емкостями $$ {C}_{1,} {C}_{2}, ...$$ общий заряд равен сумме зарядов отдельных конденсаторов, общее напряжение равно напряжению на каждом, общая ёмкость равна сумме ёмкостей:
$$ C={C}_{1}+{C}_{2}+...$$
 |
| Рис. 10.1 |
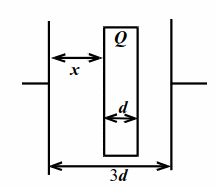
В плоский конденсатор параллельно его обкладкам вставлена пластина из диэлектрика с диэлектрической проницаемостью $$ \varepsilon $$ (рис. 10.1). Площадь обкладок конденсатора и пластины $$ S$$, толщина пластины $$ d$$, расстояние между обкладками $$ 3d$$. Найти ёмкость такого конденсатора.
Пусть расстояние от пластины до левой обкладки конденсатора $$ x$$. Наклеим мысленно на обе стороны пластины тонкую проводящую и незаряженную фольгу. От этого ничего не изменится. Обе фольги можно рассматривать как своеобразные провода, соединяющие три последовательно соединённых конденсатора с расстояниями $$ x$$, $$ d$$ и $$ 2d-x$$. Для общей ёмкости $$ C$$:
$$ {\displaystyle \frac{1}{C}}={\displaystyle \frac{x}{{\varepsilon }_{0}S}}+{\displaystyle \frac{d}{\varepsilon {\varepsilon }_{0}S}}+{\displaystyle \frac{2d-x}{{\varepsilon }_{0}S}}$$.
Окончательно $$ C={\displaystyle \frac{\varepsilon {\varepsilon }_{0}S}{d(2\varepsilon +1)}}.$$ Заметим, что не заданная в условии величина $$ x$$ «исчезла» в процессе решения.
 |
| Рис. 10.2 |
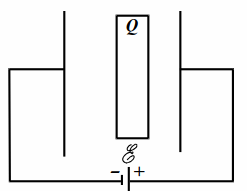
В плоский конденсатор ёмкостью $$ C$$ вставлена параллельно обкладкам плоская проводящая пластина с зарядом $$ Q$$ (рис. 10.2). Конденсатор подсоединён к источнику с ЭДС $$ \mathcal{E}$$. Площади пластины и обкладок конденсатора равны. Толщина пластины равна расстоянию от неё до правой обкладки и составляет четверть от расстояния между обкладками. Найти заряд конденсатора.
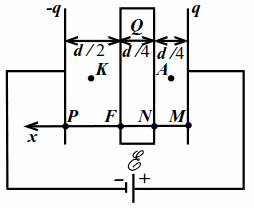
Пусть $$ d$$ – расстояние между обкладками, $$ S$$ – их площадь. Пусть $$ q$$ заряд правой обкладки. Тогда заряд левой будет $$ -q$$, т. к. заряд в значительных количествах не может накапливаться на соединительных проводах и в источнике. Направим ось $$ x$$ влево (рис. 10.3).
 |
| Рис. 10.3 |
Заметим, что поле внутри пластины отсутствует и разность потенциалов $$ {\varphi }_{N}-{\varphi }_{F}$$ между точками $$ N$$ и $$ F$$ равна нулю. Кроме того, заряды на поверхностях пластины создают вне пластины такое же поле, как и заряд $$ Q$$, если бы его расположить на любой из двух поверхностей пластины. Это легко показать отдельно.
Разность потенциалов $$ {\varphi }_{M}-{\varphi }_{P}$$ между точками $$ M$$ и $$ P$$ равна $$ \mathcal{E}$$. Поэтому
$$ ({\varphi }_{M}-{\varphi }_{N})+({\varphi }_{N}-{\varphi }_{F})+({\varphi }_{F}-{\varphi }_{P})=\mathcal{E}$$.
У нас $$ {\varphi }_{M}-{\varphi }_{N}={E}_{A}{\displaystyle \frac{d}{4}}, {\varphi }_{N}-{\varphi }_{F}=0, {\varphi }_{F}-{\varphi }_{P}={E}_{K}{\displaystyle \frac{d}{2}}$$.
Здесь - $$ {E}_{A}$$ и $$ {E}_{K}$$ - проекции напряжённости результирующего поля на ось `x`. По принципу суперпозиции полей
$$ {E}_{A}={\displaystyle \frac{q}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{Q}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{-q}{2{\varepsilon }_{0}S}}={\displaystyle \frac{1}{2{\varepsilon }_{0}S}}\left(2q-Q\right)$$,
$$ {E}_{K}={\displaystyle \frac{q}{2{\varepsilon }_{0}S}}+{\displaystyle \frac{Q}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{-q}{2{\varepsilon }_{0}S}}={\displaystyle \frac{1}{2{\varepsilon }_{0}S}}\left(2q+Q\right)$$.
Подставляя выражения для $$ {E}_{A}$$, $$ {E}_{K}$$ и разностей потенциалов в первое
уравнение, получим после упрощений $$ 6q+Q=8\mathcal{E}{\displaystyle \frac{{\varepsilon }_{0}S}{d}}$$.
Так как $$ {\displaystyle \frac{{\varepsilon }_{0}S}{d}}=C$$, то $$ q=(8C\mathcal{E}-Q)/6$$.
Следует заметить, что знак найденного заряда правой обкладки зависит от соотношения заданных в условии задачи величин.
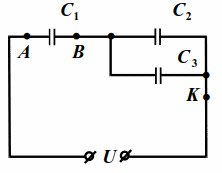 |
| Рис. 10.4 |
На схему (рис. 10.4) подано напряжение `U=24` В. Ёмкости конденсаторов `C_1=1` мкФ, $$ {C}_{2}=2$$ мкФ, $$ {C}_{3}=3$$ мкФ. Найти напряжения на конденсаторах.
В задачах, где есть схемы с конденсаторами, обычно предполагается, что схемы собраны из первоначально незаряженных конденсаторов.
Ёмкость между точками $$ B$$ и $$ K$$:
$$ {C}_{BK}={C}_{2}+{C}_{3}=5$$ мкФ.
Общая емкость: $$ {C}_{AK}={\displaystyle \frac{{C}_{1}{C}_{BK}}{{C}_{1}+{C}_{BK}}}={\displaystyle \frac{5}{6}}$$ мкФ.
Общий заряд всей батареи конденсаторов $$ {q}_{AK}={C}_{AK}U=20·{10}^{-6 }\mathrm{Кл}.$$
Так как заряд $$ {q}_{1}$$ конденсатора $$ {C}_{1}$$ равен заряду батареи, то напряжение на этом конденсаторе $$ {U}_{1}={q}_{1}/{C}_{1}={q}_{AK}/{C}_{1}=20$$ В. Напряжения на конденсаторах $$ {C}_{2}$$ и $$ {C}_{3}$$ равны напряжению между точками $$ B$$ и $$ K$$ и в сумме с $$ {U}_{1}$$ дают $$ U$$.
Поэтому $$ {U}_{2}={U}_{3}={U}_{BK}=U-{U}_{1}=4$$ В.
Приведённая в задаче схема негромоздкая, и ответ легко получить в общем виде:
$$ {U}_{1}={\displaystyle \frac{{C}_{2}+{C}_{3}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=20$$ B,
$$ U2=U3={\displaystyle \frac{{C}_{1}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=4$$ B.

Слово «электричество» может вызвать представление о сложной современной технике: компьютерах, телевизорах, электродвигателях и т. д. Но электричество играет в нашей жизни гораздо более серьёзную роль. Действительно, согласно современной теории строения вещества, силы, действующие между атомами и молекулами, в результате чего образуются жидкие и твёрдые тела, – это электрические силы. Они ответственны и за обмен веществ, происходящий в человеческом организме. Даже когда мы что-нибудь тянем или толкаем, это оказывается результатом действия электрических сил между молекулами руки и того предмета, на который мы воздействуем. И вообще, большинство сил (например, силы упругости, силы реакции опоры) сегодня принято считать электрическими силами, действующими между атомами. Сила тяжести, однако, не относится к электрическим силам.
Электрические явления известны с древних времён, но лишь в последние два столетия они были досконально изучены. По современным представлениям вся совокупность электрических и магнитных явлений есть проявление существования, движения и взаимодействия электрических зарядов. В настоящем Задании мы познакомимся с основными понятиями, определениями и законами, утвердившимися при описании электрических явлений.

По современным представлениям атом состоит из массивного положительно заряженного ядра, состоящего из протонов и нейтронов, и движущихся вокруг ядра отрицательно заряженных электронов. В нормальном состоянии положительный заряд ядра (его носителями являются находящиеся в ядре протоны) равен по величине (т. е. по модулю) отрицательному заряду электронов, и атом в целом электрически нейтрален. Однако атом может терять или приобретать один или несколько электронов. Тогда его заряд будет положительным или отрицательным, и такой атом называется ионом.
В твёрдом теле ядра атомов могут колебаться, оставаясь вблизи фиксированных положений, в то время как часть электронов движется свободно. Электризацию трением можно объяснить тем, что в различных веществах ядра удерживают электроны с различной силой. Когда пластмассовая линейка, которую натирают бумажной салфеткой, приобретает отрицательный заряд, это означает, что электроны в бумажной салфетке удерживаются слабее, чем в пластмассе, и часть их переходит с салфетки на линейку. Положительный заряд салфетки равен по величине отрицательному заряду, приобретённому линейкой. Таким образом, при электризации тел заряды не создаются, а перераспределяются. Этим и объясняется явление электризации: электроны удаляются из тела или заимствуются у атомов другого тела, но не уничтожаются и не создаются вновь. Следует заметить, что при описанном способе электризации трение не играет принципиальной роли: сдавливая тела, мы просто сближаем их поверхности, которые без этого соприкасались бы в немногих точках вследствие неровностей и выступов.
Наэлектризовать тело можно и другими способами. Например, приведя незаряженное тело в соприкосновение с заряженным. Возможна электризация через влияние, т. е. без непосредственного контакта. Опыт показывает, что под действием заряженного тела на незаряженном может происходить перераспределение электронов или упорядочение молекул (или атомов), вследствие чего части незаряженного тела оказываются наэлектризованными. Это явление получило название электризации через влияние, или электростатической индукции, а заряды, возникающие вследствие перераспределения (упорядочения), индуцированными.
Электризация у некоторых веществ может происходить под действием электромагнитных волн: электроны покидают облучаемую поверхность, в результате тело заряжается положительно. Это явление называется фотоэлектрическим эффектом, или кратко фотоэффектом.
В результате действия ультрафиолетового электромагнитного излучения на первоначально незаряженное тело его поверхность покинуло `N=4,0*10^(10)` электронов. Найдите заряд `Q` тела? Элементарный заряд `e=1,6*10^(-19)`Кл.
Положительный заряд тела будет обусловлен некомпенсированным электронами зарядом `Q=N*e=4,0*10^(10)*1,6*10^(-19)=6,4*10^(-9)`Кл.

Слово электричество происходит от греческого названия янтаря – ελεκτρον. Янтарь – это окаменевшая смола хвойных деревьев; древние заметили, что если натереть янтарь куском шерстяной ткани, то он будет притягивать лёгкие предметы и пыль. В конце XVI века английский учёный У. Гильберт обнаружил, что таким же свойством обладают стекло и ряд других веществ, натёртых шёлком. Теперь мы говорим, что в этих случаях тела, благодаря трению, приобретают электрический заряд, а сами тела называем заряженными.
Все ли электрические заряды одинаковы или существуют различные их виды? Опыт показывает, что существует два и только два вида зарядов, причём заряды одного вида отталкиваются, а заряды разных видов притягиваются. Мы говорим, что одноимённые заряды отталкиваются, а разноимённые притягиваются.
Американский учёный Б. Франклин (XVIII век) назвал эти два вида зарядов положительными и отрицательными. Какой заряд как назвать было совершенно безразлично; Франклин предложил считать заряд наэлектризованной стеклянной палочки положительным. В таком случае заряд, появляющийся на янтаре, потёртом о шерсть, будет отрицательным. Этого соглашения придерживаются и по сей день.
О заряженных телах говорят, что одни тела наэлектризованы сильнее, а другие слабее. Для того чтобы такие утверждения имели смысл, следует установить количественную меру, позволяющую сравнивать степени наэлектризованности тел. Мерой наэлектризованности любого тела является электрический заряд `Q` этого тела (латинские буквы `q` и `Q` традиционно используются для обозначения заряда). В свою очередь, незаряженные тела называют электронейтральными, или просто нейтральными, их заряд равен нулю.
В международной системе единиц (сокращенно СИ) единицей измерения заряда служит кулон (Кл) (в честь французского учёного Шарля Кулона, установившего в 1785 г. закон взаимодействия точечных зарядов). Определение этой единицы в СИ даётся через единицу измерения силы тока и будет представлено ниже.
Развитие науки о природе привело не только к открытию элементарных частиц (протонов, электронов, нейтронов и др.), но и показало, что электрический заряд не может существовать сам по себе, без элементарной частицы – носителя заряда.
Важными свойствами заряда являются его делимость и независимость от скорости.
Экспериментально установлена делимость электрического заряда и существование его наименьшей порции. Эту наименьшую величину электрического заряда называют элементарным зарядом `e=1,6*10^(-19)`Кл. Несмотря на значительные экспериментальные усилия, к настоящему времени не обнаружены в свободном состоянии носители с зарядом `|q|<e`, где `e` - элементарный заряд.
Носителями электрического заряда являются элементарные частицы, например, электроны (заряд каждого `q_e=-e=-1,6*10^(-19)`Кл), протоны (заряд каждого `q_p=e=1,6*10^(-19)`Кл). Экспериментально установлено, что отрицательный заряд электрона равен (с высокой точностью) по абсолютному значению положительному заряду протона. Величина заряда любого тела кратна элементарному заряду.
Металлическому шару путём удаления части электронов сообщается заряд `Q=2,0*10^(-6)` Кл. Сколько электронов удалено с шара? На сколько изменится масса шара? Элементарный заряд `e=1,6*10^(-19)`Кл, масса электрона `m_e=0,9*10^(-30)`кг.
Количество удалённых электронов найдём из равенства
`N=(-Q)/(-e)=(2,0*10^(-6))/(1,6*10^(-19))=1,25*10^(13)`.
Масса электронов, удалённых с шара,
`m=N*m_e=1,25*10^(13)*0,9*10^(-30)=1,125*10^(-17)`кг
даёт ответ на второй вопрос задачи. Отметим, что убыль массы шара очень мала.
Независимость элементарного заряда от скорости носителя доказывается фактом электронейтральности атомов, в которых вследствие различия масс электрона и протона лёгкие электроны, видимо, движутся значительно быстрее массивных протонов. Если бы заряд зависел от скорости, нейтральность атомов не могла бы соблюдаться. Так что независимость заряда от скорости принимается в качестве одного из экспериментальных фактов, на которых строится теория электричества.
Лишь в XIX веке стало ясно: причина существования электрического заряда кроется в самих атомах. Позднее (в другом Задании) мы обсудим строение атома и развитие представлений о нём более подробно; здесь же кратко остановимся на основных идеях, которые помогут нам лучше понять природу электричества.

По поведению зарядов в наэлектризованном теле все вещества делятся на проводники и изоляторы (диэлектрики). В диэлектриках сообщённый им заряд остаётся в том месте, куда он был помещён при электризации. В проводниках сообщённый заряд может свободно перемещаться по всему телу. Именно поэтому проводящие тела можно заряжать электризацией через влияние. Почти все природные материалы попадают в одну из этих двух резко различных категорий. Есть, однако, вещества (среди которых следует назвать кремний, германий, углерод), принадлежащие к промежуточной, но тоже резко обособленной категории. Их называют полупроводниками.
С точки зрения атомной теории электроны в изоляторах связаны с атомами очень прочно, в то время как в проводниках многие электроны связаны с атомами очень слабо и могут свободно перемещаться внутри вещества. Такие электроны называют «свободными», или электронами проводимости. Слово «свободными» взято в кавычки, так как свойства электронов в металле значительно отличаются от свойств действительно свободных электронов в вакууме. В металлических телах – проводниках электричества – число свободных электронов огромно. Проиллюстрируем это утверждение на следующем примере.
Оцените число `n` свободных электронов в `V=1"м"^3` меди, считая, что в меди в среднем в расчёте на один атом свободным является один электрон. Плотность меди `rho=8,9*10^3 "кг"//"м"^3`, в `M=64` г меди содержится `N_A=6,02*10^(23)` атомов.
Согласно условию число свободных электронов в любом объёме меди равно числу атомов в нём. Поэтому определим число атомов в объёме `V`. Для этого следует массу меди `rhoV` разделить на `M` и умножить на `N_A`, т. е.
`N=(rhoV)/M N_A=(8,9*10^3*1)/(64*10^(-3))*6,02*10^(23)~~8,4*10^(28)`.
Найденная величина называется концентрацией носителей.

Сохранение электрического заряда представляет собой важнейшее известное из опыта его свойство: в изолированной системе алгебраическая сумма зарядов всех тел остаётся неизменной. Справедливость этого закона подтверждается не только в процессах электризации, но и в наблюдениях над огромным числом рождений, уничтожений и взаимных превращений элементарных частиц. Закон сохранения электрического заряда – один из самых фундаментальных законов природы. Неизвестно ни одного случая его нарушения. Даже в тех случаях, когда происходит рождение новой заряженной частицы, обязательно одновременно рождается другая частица с равным по величине и противоположным по знаку зарядом.
Электрический заряд элементарной частицы не зависит ни от выбора системы отсчёта, ни от состояния движения частицы, ни от её взаимодействия с другими частицами. Поэтому и заряд макроскопического тела не зависит ни от движения составляющих его частиц, ни от движения тела как целого.
Два одинаковых проводящих шарика, несущих заряды `Q_1=-9,0*10^(-9)` Кл и `Q_2=2,0*10^(-9)` Кл, приводят в соприкосновение и удаляют друг от друга. Какими станут заряды `Q_1^'` и `Q_2^'` шариков?
После приведения шариков в соприкосновение заряды, свободно перемещающиеся в проводниках, придут в движение и разделятся поровну между шариками. Действительно у зарядов «нет оснований предпочесть» один из шариков: «с точки зрения зарядов» шарики неотличимы. Тогда `Q_1^'=Q_2^'`. Заряды шариков найдём по закону сохранения электрического заряда:
`Q_1+Q_2=2Q_1^'`.
Отсюда `Q_1^'=(Q_1+Q_2)/2=(-9,0*10^(-9)+2,0*10^(-9))/2=-3,5*10^(-9)` Кл.
Соображения симметрии, использованные при решении задачи, являются важнейшими в физике, к ним мы будем неоднократно обращаться в дальнейшем в различных разделах курса физики.
Свободный нейтрон `n` - незаряженная частица – распадается на протон `p`, электрон `e^-` и электронное антинейтрино $$ {\stackrel{~}{\nu }}_{e}$$. Схему этой реакции записывают в виде $$ n\to p+{e}^{-}+{\stackrel{~}{\nu }}_{e}$$. Найдите заряд `q` антинейтрино.
По условию нейтрон – незаряженная частица. Заряды протона и электрона равны соответственно `e` и `-e`. Из закона сохранения заряда следует, что заряд нейтрона равен сумме зарядов продуктов реакции, т. е. протона, электрона и антинейтрино:
`0=e+(-e)+q`.
Отсюда `q=0`.
Заряд электронного антинейтрино равен нулю.

Заряженные тела воздействуют друг на друга. Сила взаимодействия двух зарядов зависит от величин этих зарядов и от расстояния межу ними. Долгое время оставалось неясным, посредством чего взаимодействуют заряженные тела, если они не вступают в непосредственный контакт друг с другом. Кулон был убеждён, что промежуточная среда, т. е. «пустота» между зарядами никакого участия во взаимодействии не принимает.
Такая точка зрения, несомненно, была навеяна впечатляющими успехами ньютоновской теории тяготения, блестяще подтверждавшейся астрономическими наблюдениями. Однако сам Ньютон писал: «Непонятно, каким образом неодушевлённая косная материя, без посредства чего-либо иного, что нематериально, могла бы действовать на другое тело без взаимного прикосновения».
В 30-е годы XIX века английским естествоиспытателем М. Фарадеем была введена в физику идея поля как материальной среды, посредством которой осуществляется любое взаимодействие пространственно удалённых тел. М. Фарадей считал, что «материя присутствует везде, и нет промежуточного пространства, не занятого ею». Фарадей развил последовательную концепцию электромагнитного поля, основанную на идее конечной скорости распространения взаимодействия. Законченная теория электромагнитного поля в строгой математической форме была через 30 лет развита другим английским физиком, Дж. Максвеллом.
По современным представлениям электрические заряды наделяют окружающее их пространство особыми физическими свойствами – создают электрическое поле. Основным свойством поля является то, что на находящуюся в этом поле заряженную частицу, действует некоторая сила, т. е. взаимодействие электрических зарядов осуществляется посредством создаваемых ими полей. Поле, создаваемое неподвижными зарядами, не изменяется со временем и называется электростатическим.
Таким образом, электрическое поле представляет собой особый вид материи (отличный от вещества), которое создаётся электрическими зарядами и которое обнаруживается по действию на электрические заряды. Более подробно взаимодействие электрических зарядов и электрические поля, создаваемые зарядами, будут рассмотрены в десятом классе, а мы перейдём к изучению вопросов, связанных с электрическим током.

Направленное движение электрических зарядов называется электрическим током. Носителями зарядов в зависимости от типа проводника могут быть электроны и ионы. В металлических проводниках – это свободные электроны, или электроны проводимости, в гальванических ваннах, т. е. в растворах электролитов, – положительные и отрицательные ионы. Тела или вещества, в которых можно создать электрический ток, называют проводниками электрического тока. Проводниками являются все металлы, водные растворы солей или кислот, ионизованные газы.
При движении свободных заряженных частиц происходит перенос заряда. Количественной характеристикой – силой $$ I$$ тока – принято считать скорость переноса заряда через любое поперечное сечение проводника, т. е. количество заряда, перемещённого через «контрольную поверхность», на которой осуществляется подсчёт пересёкшего её заряда, в единицу времени:
`I=q/t`, (1)
где `q` – заряд, прошедший через произвольное фиксированное поперечное сечение проводника за время от `0` до `t`. Если сила тока не изменяется со временем, ток называют постоянным. Единица измерения силы тока в системе СИ называется ампером (А) (в честь А.М. Ампера – французского учёного XIX века) и вводится через магнитное взаимодействие токов.
Один ампер есть сила такого тока, поддерживаемого в двух бесконечных (очень длинных) прямолинейных параллельных проводниках ничтожно малой площади поперечного сечения, расположенных на расстоянии `1`м в вакууме, при котором в расчёте на `1` метр длины проводника действует сила `F=2*10^(-7) "Н"`.
Единица измерения силы тока ампер, наряду с метром, секундой, килограммом, является основной единицей системы СИ. Единица измерения заряда кулон (Кл) является производной и вводится в соответствии с (1): один кулон – это электрический заряд, проходящий через поперечное сечение проводника при силе тока $$ 1\mathrm{A}$$ за $$ 1\mathrm{c}$$, т. е. $$ 1\mathrm{Кл}=1\mathrm{A}·1\mathrm{c}.$$
За направление электрического тока принимают направление, в котором движутся положительно заряженные носители тока.
Отношение силы `I` тока к площади `S` поперечного сечения проводника называется плотностью тока:
`j=I/S`, (2)
которая равна силе тока в расчёте на единицу площади поперечного сечения.
По проводу течёт постоянный ток. Через произвольное поперечное сечение за время `t=2` мин протёк заряд `q=1,2` Кл. Найдите силу `I` тока в проводе и его плотность `j`. Площадь поперечного сечения проводника `S=0,5 "мм"^2`.
Силу тока определим по формуле (1):
$$ I={\displaystyle \frac{q}{t}}={\displaystyle \frac{\mathrm{1,2}}{120}}=\mathrm{0,01}\mathrm{A}$$,
плотность тока найдём по формуле (2):
`j=I/S=(0,01)/(0,5*10^(-6))=2*10^4"А"//"м"^2`.
Согласно модели, предложенной Нильсом Бором, в основном состоянии атома водорода электрон движется вокруг покоящегося протона по круговой орбите радиуса `r=0,53*10^(-10)` м со скоростью `v=2,2*10^6` м/с. Какой величине `I` тока эквивалентно движение электрона по орбите? Каково направление этого тока? Элементарный заряд `e=1,6*10^(-19)` Кл.
В рассматриваемой модели электрон обращается вокруг протона с периодом `T=(2pir)/v`. За `t=1` с электрон пересечёт любую контрольную поверхность, на которой происходит подсчёт переносимого заряда, `nu=1/T` раз. Тогда через эту поверхность за `t=1` с пройдёт заряд `q=e*nu`, т. е. сила эквивалентного тока в соответствии с (1) равна
`I=q/t=enu=ev/(2pir)=1,6*10^(-19) *(2,2*10^6)/(2*3,14*0,53*10^(-10))~~1,06*10^(-3) "А"`.
Поскольку электрон – отрицательно заряженная частица, то направление рассматриваемого тока противоположно направлению движения электронов.

Электрический ток течёт в электрических цепях, представляющих собой различные приборы и устройства, соединённые проводниками.
Если бы носители заряда, приведённые в движение в замкнутом проводнике, не взаимодействовали с ионами, то они двигались бы бесконечно долго. Такой ток можно наблюдать в некоторых веществах при весьма низких температурах; удельное сопротивление таких веществ – их называют сверхпроводниками – равно нулю при этих температурах.
Но в большинстве проводников при протекании тока движущиеся заряженные частицы взаимодействуют с неподвижными и теряют кинетическую энергию.
Для получения постоянного тока, т. е. не изменяющегося с течением времени, на заряды в электрической цепи должны действовать не только силы электрического поля, но и другие силы, отличные от сил электрического взаимодействия. Такие силы получили общее название сторонних электродвижущих сил. Всякое устройство, в котором возникают сторонние силы, называют источником тока. Источниками тока являются, например, батарейки, аккумуляторы и т. д.
Сторонние силы в источниках возникают по разным причинам. В химических источниках, например, в автомобильном аккумуляторе или в гальваническом элементе, они возникают благодаря химическим реакциям в области контакта пластин аккумулятора или электродов батарейки с жидким электролитом. В фотоэлементе они возникают в результате действия электромагнитного излучения на электроны в металле или полупроводнике. В генераторах на электростанции сторонние силы возникают в проводниках при движении их в магнитном поле.
Если воспользоваться гидростатической аналогией, то силы электрического поля в электрической цепи можно уподобить силе тяжести, стремящейся выравнивать уровни жидкости в сообщающихся сосудах; источник тока с действующими в нём сторонними электродвижущими силами можно сравнить с насосом, работающим против силы тяжести и восстанавливающим разность уровней в сосудах, несмотря на течение жидкости.
Источник тока по результатам своего действия представляет собой устройство, отделяющее положительные заряды от отрицательных. После разделения заряды перемещаются на полюса (электроды) источника. При этом один из электродов заряжается положительно, другой отрицательно. И если к источнику подключить проводник, то эти заряды действуют на заряды проводника вблизи полюсов, те в свою очередь действуют на соседние и т. д. В результате этих коллективных взаимодействий в цепи на поверхности проводника возникает такое распределение зарядов, которое обеспечивает существование внутри проводника электрического поля, а в проводнике под действием сил этого поля течёт электрический ток.

В электрической цепи, подключённой к источнику, возникают электрические силы, действующие на носители зарядов и приводящие их в движение. Пусть под действием электрической силы `F` частица, несущая заряд `q`, переместилась вдоль проводника из точки `1` в точку `2`, а сила `F` совершила над заряженной частицей работу `A_(12)`. Отношение работы `A_(12)` электрической силы над зарядом `q` при перемещении его из точки `1` в точку `2` к самому заряду $$ q$$ называют электрическим напряжением между точками `1` и `2`:
`U_(12)=(A_(12))/q`. (3)
Единицей измерения напряжения в СИ является вольт (В).
За один вольт принимается напряжение на концах проводника, при котором работа сил электрического поля по перемещению через этот проводник заряда в один кулон равна одному джоулю.
Эта единица названа в честь итальянского физика А. Вольта, который в 1800 г. изобрёл электрическую батарею и впервые получил с её помощью постоянный ток, устойчиво поддерживавшийся в электрической цепи. Это открытие ознаменовало начало новой эпохи, полностью преобразившей нашу цивилизацию: современная жизнь немыслима без использования электрического тока.
В соотношении (3) индексы `1` и `2` можно опустить, если помнить, что `1` – это точка «старта», `2` – точка «финиша».
Зная напряжение `U` на концах проводника и силу тока `I`, текущего в проводнике в течение времени `t` постоянного тока, вычислим заряд `q=I*t`, который протечёт за указанное время по проводнику. Тогда за это время силы электрического поля в проводнике совершат работу
`A=q*U=I*t*U`. (4)
Это позволяет судить о скорости совершения работы электрическими силами, т. е. о мощности, развиваемой силами электрического поля. Из (4) следует, что в проводнике, напряжение на концах которого равно `U`, а сила тока `I`, силы электрического поля в единицу времени совершают работу
`P=A/t=I*U`. (5)
Напомним, что единицей измерения мощности в СИ служит ватт (Вт).
Очень часто работу и мощность электрических сил называют соответственно работой и мощностью электрического тока, тем самым подчёркивают, что это работа по поддержанию электрического тока в цепи.
По проводнику в течение `T=1` мин течёт постоянный ток силой `I=0,2` А. Напряжение на проводнике `U=1,5` В. Какую работу `A` совершают электрические силы в проводнике за указанное время? Найдите мощность `P` электрического тока в проводнике.
За время `T` через проводник пройдёт заряд `Q=I*T`. Работа сил электрического поля над этим зарядом в соответствии с (4) равна
`A=Q*U=I*T*U=0,2*60*1,5=18` Дж.
Для ответа на второй вопрос задачи воспользуемся соотношением (5):
`P=I*U=0,2*1,5=0,3` Вт.
Заметим, что в повседневной жизни, рассчитываясь «за электричество», мы оплачиваем расход электроэнергии – работу электрических сил, а не мощность. И здесь принято работу электрических сил выражать во внесистемных единицах – киловатт-часах:
`1` кВт`*`ч`=1000`Вт`*3600`с`=3,6*10^6`Дж
Работа электрического тока может идти на изменение механической и внутренней энергий проводника. Например, в результате протекания электрического тока через электродвигатель его ротор (подвижная часть, способная вращаться, в отличие от статора) раскручивается. При этом большая часть работы электрических сил идёт на увеличение механической энергии ротора, а также других тел, с которыми ротор связан теми или иными механизмами. Другая часть работы электрического тока (в современных электродвигателях один – два процента) идёт на изменение внутренней энергии обмоток двигателя, что приводит к их нагреванию (обмотка электродвигателя представляет собой катушку, изготовленную обычно из меди, с большим числом витков).
Обсудим тепловое действие электрического тока более подробно. Из опыта известно, что электрический ток нагревает проводник. Объясняется это явление тем, что свободные электроны в металлах, перемещаясь под действием сил электрического поля, взаимодействуют с ионами вещества и передают им свою энергию. В результате увеличивается энергия колебаний ионов в проводнике, его температура растёт, при этом говорят, что в проводнике за некоторое время `t` выделяется количество теплоты `Q_("тепл")`. Если проводник с током неподвижен и величина тока постоянна, то работа электрических сил идёт на изменение внутренней энергии проводника. По закону сохранения энергии это количество равно работе сил электрического поля (4) в проводнике за то же самое время, т. е.
`Q_("тепл")=I*t*U`. (6)
Отсюда мощность `P` тепловыделения, т. е. количество теплоты, выделяющейся в единицу времени на участке цепи, где напряжение равно `U`, а сила тока равна `I` составляет
`P=(Q_("тепл"))/t=U*I`. (7)
По спирали электроплитки, подключённой к источнику с напряжением `U=120` В, протекает постоянный ток силой `I=5` А в течение `T=1` ч. Какое количество теплоты `Q_("тепл")` отдаёт при этом плитка в окружающую среду?
В окружающую среду будет передано то количество теплоты, которое выделится в спирали нагревательного элемента плитки за указанное время. По формуле (6) находим:
`Q_("тепл") =I*T*U=5*3600*120=2,16*10^6` Дж.
Электродвигатель, включённый в электрическую сеть с напряжением `U=24` В, за время `T=1` ч работы совершил механическую работу `A=1680` кДж. Сила тока в обмотке `I=20` А. Найдите мощность `P` электрического тока и коэффициент полезного действия `eta` двигателя. Какое количество теплоты `Q_("тепл")` выделится в обмотке?
Мощность электрического тока найдём по формуле (5):
`P=I*U=20*24=480` Вт.
По определению коэффициент полезного действия (КПД) `eta` двигателя равен отношению полезной механической работы `A` к работе электрических сил `A_("эл")`, умноженному на `100%`. С учётом выражения (4) для работы электрических сил находим КПД электродвигателя:
`eta=A/(A_("эл"))*100%=A/(UIT)*100%=(1680*10^3)/(24*20*3600)*100%~~97%`.
Количество `Q_("тепл")` теплоты, выделившейся в обмотке, найдём по закону сохранения энергии `A_("эл")=A+Q_("тепл")`. Отсюда `Q_("тепл")=A_("эл")-A=UIT-A=24*20*3600-1680*10^3=48*10^3` Дж.

Как отмечалось выше, для поддержания постоянного тока в проводнике, т. е. движения электронов с постоянной скоростью, необходимо непрерывное действие сил электрического поля на носители заряда. Это означает, что электроны в проводниках движутся «с трением», иначе говоря, проводники обладают электрическим сопротивлением.
Если состояние проводника остаётся неизменным (не изменяется его температура и т. д.), то для каждого проводника существует однозначная зависимость между напряжением `U` на концах проводника и силой `I` тока в нём `I=f(U)`. Она называется вольтамперной характеристикой данного проводника.
Для многих проводников эта зависимость особенно проста – линейная: сила тока прямо пропорциональна приложенному напряжению, т. е.
`I=1/RU`, (8)
где `R` – электрическое сопротивление проводника (постоянная при неизменных условиях величина).
Этот закон носит название закона Ома. Немецкий физик Г. Ом в 1827 г. в результате серии экспериментов установил, что для широкого класса проводников сила `I` электрического тока в проводнике пропорциональна напряжению `U` на концах проводника.
Сопротивление `R` проводника зависит от рода вещества проводника, от его размеров и формы, а также от состояния проводника.
Единицей сопротивления в СИ является один Ом (Ом). За один Ом принимается сопротивление такого проводника, в котором при напряжении между его концами один вольт течёт постоянный ток силой один ампер: `1`Ом`=1`В`//1`A.
Вытекающее из закона Ома (8) соотношение
`R=U/I` (9)
можно рассматривать и как определение сопротивления по приведённой формуле.
Г. Ом установил, что для проводников $$ R$$ не зависит от $$ U.$$
В технических приложениях для описания процессов в электрических цепях часто используется понятие вольтамперной характеристики. Для проводников, подчиняющихся закону Ома (8), графиком зависимости силы `I` тока в проводнике от напряжения `U` на нём будет прямая линия, проходящая через начало координат (см. рис. 1). При этом говорят, что проводник имеет линейную вольтамперную характеристику.
В то же время для полупроводников, электронных ламп, диодов, транзисторов зависимость `I=f(U)` носит сложный характер, и такие элементы называют нелинейными (или неомическими). Для таких элементов величина `R`, вычисленная по формуле `R=U/I`, зависит от `U`. В частности, при измерении вольтамперной характеристики лампочки накаливания с вольфрамовой нитью мы обнаружим, что она имеет вид, схематически показанный на рис. 2. Искривление вольтамперной характеристики связано с нагревом нити и увеличением сопротивления нити накала с ростом температуры. В некоторых устройствах, таких как диод, сопротивление зависит от направления тока.
Обсудим вопрос о тепловыделении в проводнике. С учётом закона Ома (8) формула (7) для мощности тепловыделения принимает вид:
`P=U*I=U^2/R=I^2R`. (10)
Другими словами, если через резистор `R` протекает постоянный ток силой `I`, то за `t` секунд в резисторе выделяется количество теплоты, равное
`Q_("тепл")=P*t=U^2/R*t=I^2*R*t`. (11)
Соотношения (10), (11) являются математическим выражением закона, открытого в XIX веке практически одновременно и независимо английским физиком Д. Джоулем и русским физиком Э.Х. Ленцем.
Обратим внимание, что полученный закон является прямым следствием закона сохранения энергии в применении к движению электрических зарядов под действием сил электрического поля.

Причиной электрического сопротивления является взаимодействие электронов с ионами кристаллической решётки. Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, на опытах изучил Г. Ом. Он установил, что сопротивление проволоки длиной `l` и площадью поперечного сечения `S` определяется по формуле
`R=rho l/S` (12)
где `rho` – удельное сопротивление вещества, из которого изготовлен проводник. Эту величину определяют экспериментально, результаты измерений удельного сопротивления приводят в физических справочниках (и в справочных разделах задачников по физике).
В соответствии с формулой (12) единицей удельного сопротивления в СИ служит Ом`*`м.
Удельное сопротивление вещества зависит от температуры. Для металлов с ростом температуры растёт и удельное сопротивление. У электролитов наблюдается обратная зависимость. Эти обстоятельства следует учитывать на практике при расчётах спиралей электронагревательных приборов, нитей лампочек накаливаний и т. д.
Резистор сопротивлением `R=38` Ом изготовлен из медного провода кругового сечения массой `m=11,2` г. Найдите длину `l` провода. Удельное сопротивление меди `rho=1,7*10^(-8)` Ом`*`м, плотность меди `delta=8,9*10^3 "кг"//"м"^3`. Обратите внимание, что в настоящем примере приняты обозначения: `delta` – плотность, `rho` – удельное сопротивление.
Обозначим площадь поперечного сечения проводника `S`. Тогда объём проводника равен `V=S*l`, его масса `m=delta*V=delta*S*l`. По формуле (12) сопротивление проводника равно `R=rhol/S`.
Исключая `S` из двух последних соотношений, приходим к ответу на вопрос задачи:
`l=sqrt((mR)/(rho delta))=sqrt((11,2*10^(-3)*38)/(1,7*10^(-8)*8,9*10^3))~~53` м.

В электрических цепях, с которыми мы встречаемся на практике, проводники могут быть соединены различными способами. Наиболее простые способы соединения известны как последовательное и параллельное соединения резисторов.
Рассмотрим участок $$ AB$$ цепи, в котором резисторы с сопротивлениями `R_1` и `R_2` соединены последовательно (рис. 3). Поставим вопрос: каким сопротивлением `R_("экв")`, подключённым между точками `A` и `B`, можно заменить последовательно соединенные сопротивления `R_1` и `R_2` так, чтобы напряжение на участке `AB` и сила тока, текущего от `A` к `B`, остались неизменными?
Для ответа на поставленный вопрос заметим, что при последовательном соединении сила тока во всех проводниках одинакова – иначе заряды накапливались бы (или исчезали) в каких-то точках цепи. Так что `I=I_1=I_2`.
Далее: работа сил электрического поля над любым зарядом при перемещении его из `A` в `B` будет равна сумме работ электрических сил над этим зарядом, совершаемых силами поля при его перемещении в каждом проводнике.
Отсюда следует, что напряжение на `AB` равно сумме напряжений на резисторах
$$ {U}_{AB}={U}_{1}+{U}_{2}=I·\left({R}_{1}+{R}_{2}\right).$$
В эквивалентной схеме сила $$ I$$ тока и напряжение $$ {U}_{AB}$$ «не заметили» замены `R_1` и `R_2` на `R_("экв")`. В этом случае по закону Ома `U_(AB)=I*R_("экв")`. Из сопоставления двух последних равенств находим
`R_("экв")=R_1+R_2`. (13)
Этот результат легко обобщается на случай `n` последовательно соединённых резисторов `R_1,R_2,...,R_n`. В этом случае (рекомендуем лично выполнить соответствующий вывод):
`R_("экв")=sum_(i=1)^n R_i=R_1+R_2+...+R_n`.
Рассмотрим теперь участок `AB` цепи, в котором резисторы с сопротивлениями `R_1` и `R_2` соединены параллельно (см. рис. 4). Поставим вопрос: каким сопротивлением `R_("экв")`, подключённым между точками `A` и `B`, можно заменить параллельно соединённые `R_1` и `R_2` так, чтобы напряжение на участке `AB` и сила тока, текущего к узлу `A` и вытекающего из узла `B` остались неизменными?
Для ответа на поставленный вопрос заметим, что при параллельном соединении проводников работа сил электрического поля в расчёте на единичный заряд (см. (3)) в проводниках одинакова (иначе нарушался бы закон сохранения энергии). Это означает, что напряжения на параллельно соединённых проводниках одинаковы. Обозначим его `U_(AB)`. Силу тока в каждом проводнике определим по закону Ома: `I_1=(U_(AB))/R_1`, `I_2=(U_(AB))/R_2`.
Далее, в любом узле, т. е. точке, где сходятся более двух проводов, по закону сохранения электрического заряда сумма токов, втекающих в узел, равна сумме токов, вытекающих из него. Отсюда следует, что в рассматриваемой задаче (рис. 4) сила `I` тока на входе и на выходе равна сумме сил токов в отдельных ветвях параллельной цепи:
`I=I_1+I_2=(U_(AB))/R_1+(U_(AB))/R_2=U_(AB)(1/R_1+1/R_2)`.
В эквивалентной схеме сила $$ I$$ тока и напряжение $$ {U}_{\mathrm{AB}}$$ связаны с `R_("экв")` законом Ома (8) `I=(U_(AB))/R_"экв"`. Два последних равенства справедливы при любых значениях, входящих в них величин `I` и `U_(AB)` если
`1/(R_("экв"))=1/R_1+1/R_2`. (14)
Этот результат легко обобщается на случай `n` параллельно соединённых резисторов `R_1, R_2, ..., R_n`. В этом случае
`1/(R_("экв"))=1/R_1+1/R_2+...+1/R_n`.
Между точками `A` и `B` электрической цепи подключены резисторы `R_1=10` Ом, `R_2=20` Ом, `R_3=30` Ом, как показано на рис. 5. Найдите эквивалентное сопротивление `R_(AB)` этого участка цепи.
Эквивалентное сопротивление `R_(12)` цепочки последовательно соединённых резисторов `R_1` и `R_2` найдём по формуле (13)
`R_(12)=R_1+R_2`.
Заменяя эти резисторы эквивалентным сопротивлением, получаем участок цепи, в котором к точкам `A` и `B` параллельно присоединены резисторы `R_(12)` и `R_3`. Тогда искомое эквивалентное сопротивление найдём из (14)
`1/(R_("экв"))=1/(R_(12))+1/(R_3)`,
`R_("экв")=(R_(12)R_3)/(R_(12)+R_3)=((R_1+R_2)R_3)/(R_1+R_2+R_3)=((10+20)30)/(10+20+30)=15`Ом.
Лестничная цепь состоит из последовательности `N` одинаковых звеньев (рис. 6 а). Последнее звено замкнуто резистором `R`. При какой величине отношения `R/r` сопротивление цепи не зависит от числа звеньев?
Сопротивление цепи не будет зависеть от числа звеньев, если эквивалентное сопротивление последнего звена (рис. 6 б) будет равно `R`. Из решения предыдущей задачи получаем:
`1/R=1/r+1/(r+R)`.
Отсюда находим `R/r=(sqrt5-1)/2~~0,618`.

Для измерения токов и напряжений в электрических цепях используются амперметры и вольтметры, основным элементом которых служит гальванометр – прибор, предназначенный для измерения величин токов. Эти измерения могут быть основаны на одном из действий тока: тепловом, физическом, химическом. Гальванометр, градуированный на величину тока, называется амперметром. По закону Ома (8) напряжение и сила тока связаны прямо пропорциональной зависимостью, поэтому гальванометр можно градуировать и на напряжение. Такой прибор называют вольтметром.
В этом задании мы не будем касаться вопросов, связанных с конкретным устройством электроизмерительных приборов, с их системами и принципами работы. Остановимся лишь на требованиях, предъявляемых к внутренним сопротивлениям амперметров и вольтметров. Важно, чтобы при включении в цепь для измерений эти приборы вносили как можно меньшее искажение в измеряемую величину.
Амперметр включается в цепь последовательно. Если сопротивление амперметра `R_"а"` и его подключают к участку цепи с сопротивлением `R_"ц"` (рис. 7а), то эквивалентное сопротивление участка цепи и амперметра в соответствии с (13) равно `R=R_"ц"+R_"а"=R_"ц"(1+(R_"а")/(R_"ц"))`.
Отсюда следует, что амперметр не будет заметно изменять сопротивление участка цепи, если его собственное (внутреннее) сопротивление будет мало по сравнению с сопротивлением участка цепи.
Чтобы добиться этого, гальванометр снабжают шунтом (синоним – добавочный путь): вход и выход гальванометра соединяются некоторым сопротивлением, обеспечивающим параллельный гальванометру дополнительный путь для тока (рис. 7 б). Поэтому внутреннее сопротивление амперметра меньше, чем у применённого в нём гальванометра. (Читателю рекомендуется лично убедиться в этом с помощью соотношения (14).) Амперметр называется идеальным, если его внутреннее сопротивление можно считать равным нулю.
Вольтметр подключается к электрической цепи параллельно тому участку, напряжение на котором требуется измерить. Присоединив, например, вольтметр с сопротивлением `R_"в"` параллельно лампочке с сопротивлением `R_"л"` (рис. 8 а), получим участок цепи, эквивалентное сопротивление которого вычисляется по формуле (14) `R=R_"л" (R"в")/(R_"л"+R_"в")`.
Отсюда следует, что чем больше сопротивление вольтметра по сравнению с сопротивлением лампочки, тем меньше эквивалентное сопротивление будет отличаться от сопротивления лампочки. Вывод: чтобы процесс измерения меньше искажал значение измеряемого напряжения, собственное (внутреннее) сопротивление вольтметра должно быть как можно больше. Поэтому в вольтметре последовательно гальванометру включают некоторое сопротивление (рис. 8б). Внутреннее сопротивление такого вольтметра, как правило, во много раз больше сопротивления входящего в него гальванометра. Вольтметр называется идеальным, если его внутреннее сопротивление можно считать бесконечно большим.
Каждый измерительный прибор рассчитан на определённый интервал значений измеряемой величины. И в соответствии с этим проградуирована его шкала. Для расширения пределов измерений в амперметре можно использовать добавочный шунт, а в вольтметре – добавочное сопротивление. Найдём значения этих сопротивлений, увеличивающих максимальную измеряемую величину тока или напряжения в раз.

Если амперметр рассчитан на силу тока `I_m`, а с его помощью необходимо измерять силу тока в `n` раз большую (см. рис. 9), то в этом случае, подключив параллельно амперметру шунт, разделим ток силой `nI_m` на два тока: один из них силой `I_m` будет течь через амперметр, тогда через шунт будет протекать ток силой `I_"ш"=(n-1)I_m`.
Поскольку шунт включён параллельно амперметру, то напряжения на шунте `U_"ш"=(n-1)I_mR_"ш"` и амперметре `U_"А"=I_mR_"А"` равны. Из равенства напряжений
`I_mR_"А"=(n-1)I_mR_"ш"`
находим
`R_"ш"=(R_"А")/(n-1)` (15)

Если вольтметр рассчитан на максимальное напряжение `U_max`, а с его помощью необходимо измерять напряжение, в `n` раз большее, то, подключив последовательно с вольтметром добавочное сопротивление `R_2` (рис. 10), разделим напряжение `n*U_max` на два слагаемых: одно из них – это напряжение $$ {U}_{\mathrm{max}}$$ на вольтметре, второе – напряжение $$ \left(n-1\right){U}_{\mathrm{max}}$$ на добавочном сопротивлении.
Поскольку добавочное сопротивление включено последовательно с вольтметром, то через вольтметр и добавочное сопротивление течёт одинаковый ток, т. е. справедливо равенство
`(U_max)/(R_"в")=((n-1)U_max)/(R_"д")`.
Отсюда
`R_"д"=(n-1)R_"в"`. (16)
Шкала гальванометра имеет `N=100` делений, цена деления $$ \delta =1\mathrm{мкА}.$$. Внутреннее сопротивление гальванометра $$ {R}_{G}=\mathrm{1,0} \mathrm{кОм}.$$. Как из этого прибора сделать вольтметр для измерения напряжений до $$ U=100 \mathrm{В}$$ или амперметр для измерения токов силой до $$ I=1\mathrm{A}$$?
Максимально допустимый ток `I_max` через гальванометр равен цене деления, умноженной на число делений: `I_max=delta*N=1*100=100` мкА. При максимальном токе напряжение на приборе максимально и по закону Ома (8) равно
`U_max=I_max*R_G=10^(-4)*10^3=0,1` В.
Для использования этого гальванометра в качестве амперметра для измерения токов силой до `I=1` А необходимо параллельно с ним включить шунт, сопротивление которого найдём по формуле (15):
$$ {R}_{\mathrm{ш}}={\displaystyle \frac{{R}_{\mathrm{G}}}{n-1}}={\displaystyle \frac{{R}_{\mathrm{G}}}{{\displaystyle \frac{I}{{I}_{\mathrm{max}}}}-1}}={\displaystyle \frac{{10}^{3}}{{\displaystyle \frac{1}{{10}^{-4}}}-1}}\approx \mathrm{0,1} \mathrm{Ом}.$$
В этом случае максимальному отклонению стрелки на шкале гальванометра соответствует ток в цепи силой `I=1` А.
Для использования этого гальванометра в качестве вольтметра для измерения напряжений до `U=100` В необходимо последовательно с ним включить добавочное сопротивление, величину которого найдём из (16):
`R_"д"=(U/U_max -1)R_G=((100)/(0,1)-1)*10^3=999` кОм.
В этом случае максимальному отклонению стрелки на шкале гальванометра соответствует напряжение между точками подключения `U=100` В.
Для измерения сопротивления `R` проводника собрана электрическая цепь, показанная на рис. 11. Вольтметр `V` показывает напряжение `U_V=5` В. Показание амперметра `A` равно `I_A=25` мА. Найдите величину `R` сопротивления проводника. Внутренне сопротивление вольтметра `R_V=1,0` кОм. Внутреннее сопротивление амперметра `R_A=2,0` Ом.
Ток `I_A`, протекающий через амперметр, равен сумме токов `I_V` и `I_R`, протекающих через вольтметр и амперметр соответственно. Напряжения на резисторе `U_R=I_R*R` и вольтметре `U_V=I_V*R_V` одинаковы и равны показанию `U_V` вольтметра. Таким образом, приходим к системе уравнений
$$ \left\{\begin{array}{l}{I}_{A}={I}_{V}+{I}_{R},\\ {U}_{V}={I}_{V}·{R}_{V}={I}_{R}·R,\end{array}\right.$$
решение которой
$$ R={\displaystyle \frac{{U}_{V}}{{I}_{A}-{\displaystyle \frac{{U}_{V}}{{R}_{V}}}}}={\displaystyle \frac{5}{25·{10}^{-3}-{\displaystyle \frac{5}{{10}^{3}}}}}=250 \mathrm{Ом}.$$
определяет величину `R` сопротивления проводника по результатам измерений. Заметим, что для приведённой схемы величина внутреннего сопротивления амперметра оказалась несущественной: `R_A` не входит в ответ.



