называется явление перераспределения зарядов проводника, вызванное влиянием внешнего электростатического поля.

1. Электростатическое поле внутри проводника отсутствует. Доказательство от противного: при наличии поля свободные заряды придут в движение, и нарушится равновесие.
2. Напряжённость поля вблизи поверхности проводника и снаружи проводника перпендикулярна поверхности. Другими словами, силовые линии входят в проводник и выходят из него перпендикулярно поверхности проводника. Доказательство от противного: в противном случае появится составляющая силы вдоль поверхности, действующая на свободные заряды на поверхности проводника, заряды придут в движение и равновесие нарушится.
3. Плотность объёмного заряда (объёмная плотность заряда), т. е. заряд единицы объёма, внутри проводника равна нулю. Доказательство от противного: пусть сколь угодно малый макроскопический объём внутри проводника заряжен положительно (отрицательно), тогда из него выходят (входят) силовые линии, т. е. вблизи этого объёма есть электрическое поле – противоречие с тем, что поле внутри проводника отсутствует.
4. Внутренность проводника не заряжена, весь заряд проводника сосредоточен на его поверхности. Это утверждение следует из равенства нулю плотности объёмного заряда.
5. Разность потенциалов любых двух точек проводника, включая точки поверхности, равна нулю. Это значит, что потенциал всех точек проводника один и тот же. Поэтому говорят о потенциале проводника, не указывая конкретной точки проводника.
Для доказательства возьмём две произвольные точки проводника и перенесём пробный заряд из одной точки в другую по произвольной траектории, лежащей внутри проводника. Поля внутри проводника нет, на пробный заряд со стороны поля сила не действует, работа сил поля над зарядом равна нулю. Тогда, согласно (5.1), разность потенциалов между этими точками тоже равна нулю.
6. Сделаем внутри проводника полость, изъяв содержимое. Изъятие нейтрального содержимого полости не вызовет изменения поля во всех точках вне и внутри проводника и в полости. Значит, не изменится распределение зарядов по поверхности проводника, а напряжённость поля внутри проводника и в полости будет равна нулю. Итак, полые проводники ведут себя точно так же, как и сплошные.

Снаружи проводящего шара с зарядом $$ Q>0$$ находится точечный заряд $$q>0$$ на расстоянии $$ R$$ от центра шара. Можно ли найти силу взаимодействия зарядов по формуле $$ F=kQq/{R}^{2}$$ ?

Из-за явления электростатической индукции заряды на поверхности шара перераспределятся, удалившись от $$ q$$. Сила станет меньше, чем рассчитанная по предложенной формуле! Этой формулой можно было бы воспользоваться, если бы заряд на поверхности шара остался равномерно распределённым.

Две проводящие пластины с зарядами $$ Q$$ и $$ 3Q$$ расположены параллельно и напротив друг друга. Площади пластин одинаковы, их размеры велики по сравнению с расстоянием между ними и можно считать, что заряды распределены по каждой поверхности пластин равномерно. Найти заряды на поверхностях пластин.

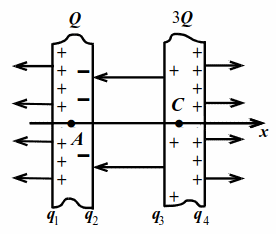Рис.8.1

Пусть площадь пластин `S`, а заряды на поверхностях пластин  $$ {q}_{1,} {q}_{2,} {q}_{3,} {q}_{4}$$ (рис. 8.1). Внутри проводящих пластин зарядов нет, заряды $$ Q$$ и $$ 3Q$$ распределены по поверхностям пластин:

$$ {q}_{1}+{q}_{2}=Q$$, $$ {q}_{3}+{q}_{4}=3Q$$.

Направим ось `x` перпендикулярно пластинам. Для любой точки вне и внутри пластин сумма напряжённостей полей, созданных зарядами $$ {q}_{1,} {q}_{2,} {q}_{3}$$ и $$ {q}_{4}$$ равна напряженности `vecE` результирующего поля:

 $$ \overrightarrow{{E}_{1}}+\overrightarrow{{E}_{2}}+\overrightarrow{{E}_{3}}+\overrightarrow{{E}_{4}}=\overrightarrow{E}$$.

Для точек $$ A$$ и $$ C$$, в которых напряжённость поля равна нулю, последнее векторное равенство, записанное в проекциях на ось $$ x$$, принимает вид:

$$ {\displaystyle \frac{{q}_{1}}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{{\displaystyle {q}_{2}}}{{\displaystyle 2{\varepsilon }_{0}S}}}-{\displaystyle \frac{{\displaystyle {q}_{3}}}{{\displaystyle 2{\varepsilon }_{0}S}}}-{\displaystyle \frac{{\displaystyle {q}_{4}}}{{\displaystyle 2{\varepsilon }_{0}S}}}=0$$,

$$ {\displaystyle \frac{{\displaystyle {q}_{1}}}{{\displaystyle 2{\varepsilon }_{0}S}}}+{\displaystyle \frac{{\displaystyle {q}_{2}}}{{\displaystyle 2{\varepsilon }_{0}S}}}+{\displaystyle \frac{{\displaystyle {q}_{3}}}{{\displaystyle 2{\varepsilon }_{0}S}}}-{\displaystyle \frac{{\displaystyle {q}_{4}}}{{\displaystyle 2{\varepsilon }_{0}S}}}=0$$.

Решая систему из четырёх записанных скалярных уравнений, находим

$$ {q}_{1}={q}_{4}=2Q$$, $$ {q}_{2}=-Q$$, $$ {q}_{3}=Q$$.

Полученный ответ справедлив при любом знаке $$ Q$$. На рис. 8.1 показана картина силовых линий и распределение зарядов для случая $$ Q>0$$.

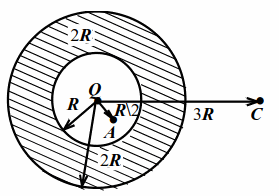Рис. 8.2

Проводящий полый шар (рис. 8.2) с радиусами сферических поверхностей $$ R$$ и $$ 2R$$ имеет заряд $$ 2Q$$ ($$ Q>0$$). В центре шара находится точечный заряд $$ Q$$. Найти напряжённость и потенциал в точках $$ A$$ и $$ C$$ на расстояниях $$ R/2$$ и $$ 3R$$ от центра шара. Найти потенциал полого шара.

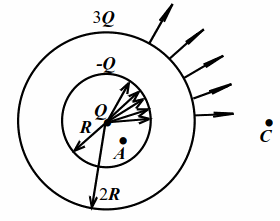Рис.8.3

Все силовые линии, вышедшие из точечного заряда $$ Q$$, заканчиваются на внутренней поверхности полого шара (на рис. 8.3 показана только часть силовых линий). Поэтому заряд на внутренней поверхности равен по модулю и противоположен по знаку заряду $$ Q$$, т. е. равен $$ -Q$$. Так как заряд проводника может располагаться только на его поверхностях и суммарный заряд равен $$ 2Q$$, то заряд внешней поверхности шара составит $$ 3Q$$. Итак, имеем систему зарядов, состоящую из точечного заряда $$ Q$$ и зарядов  $$ -Q$$ и $$ 3Q$$ на сферах радиусами $$ R$$ и $$ 2R$$.

Для точек $$ A$$ и $$ C$$ по принципу суперпозиции полей проекция напряжённости результирующего поля на ось $$ x$$, проведённую из центра шара через исследуемую точку (для точек $$ A$$ и $$ C$$ оси $$ x$$ различны), равна сумме проекций напряжённостей полей, созданных зарядами $$ Q$$, $$ -Q$$, $$ 3Q$$:

$$ {E}_{Ax}=k{\displaystyle \frac{Q}{{\left(R/2\right)}^{2}}}+0+0=4k{\displaystyle \frac{Q}{{R}^{2}}}>0$$,

$$ {E}_{Cx}=k{\displaystyle \frac{Q}{{\left(3R\right)}^{2}}}+k{\displaystyle \frac{-Q}{{\left(3R\right)}^{2}}}+k{\displaystyle \frac{3Q}{{\left(3R\right)}^{2}}}={\displaystyle \frac{1}{3}}k{\displaystyle \frac{Q}{{R}^{2}}}>0$$.

Проекции получились положительные. Это значит, что напряжённости поля в точках $$ A$$ и $$ C$$ направлены от центра шара и равны

$$ {E}_{A}=4k{\displaystyle \frac{Q}{{R}^{2}}}$$, $$ {E}_{C}={\displaystyle \frac{1}{3}}k{\displaystyle \frac{Q}{{R}^{2}}}$$.

Найдём потенциалы. По принципу суперпозиции полей потенциал в т. `A` равен сумме потенциалов в этой точке от полей, созданных зарядами $$ Q$$, $$ -Q$$, $$ 3Q$$:

$$ {\varphi }_{A}=k{\displaystyle \frac{Q}{R/2}}+k{\displaystyle \frac{-Q}{R}}+k{\displaystyle \frac{3Q}{2R}}={\displaystyle \frac{5}{2}}k{\displaystyle \frac{Q}{R}}$$.

Аналогично потенциал в т. $$ C$$ :

$$ {\varphi }_{C}=k{\displaystyle \frac{Q}{3R}}+k{\displaystyle \frac{-Q}{3R}}+k{\displaystyle \frac{3Q}{3R}}=k{\displaystyle \frac{Q}{R}}$$.

Потенциал шара проще всего найти, определив потенциал наружной
поверхности шара:

$$ \varphi =k{\displaystyle \frac{Q}{2R}}+k{\displaystyle \frac{-Q}{2R}}+k{\displaystyle \frac{3Q}{2R}}={\displaystyle \frac{3}{2}}k{\displaystyle \frac{Q}{R}}$$.