Автор
Чивилев Виктор Иванович 1358 статей

§ 6. Потенциал поля точечного заряда и заряда, равномерно распределённого по сферической поверхности

Примем потенциал бесконечности равным нулю. Тогда, используя (5.2), можно вывести, что на расстоянии $$ r$$ от точечного заряда $$ Q$$ потенциал электростатического поля:

$$ \varphi =k{\displaystyle \frac{Q}{r}}$$. (6.1)
Рис. 6.1


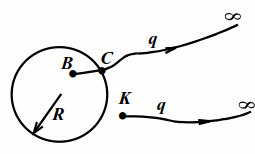
Возьмём теперь заряд $$ Q$$, равномерно распределённый по сфере радиуса $$ R$$ (рис. 6.1). 

Для нахождения потенциала на расстоянии $$ r$$ от центра сферы перенесём мысленно пробный заряд $$ q$$ из исследуемой точки в бесконечность и применим формулу (5.2). Для произвольной точки $$ K$$ вне сферы $$ {\varphi }_{K}={A}_{K\infty }/q$$, где $$ {A}_{K\infty }$$ – работа сил поля над $$ q$$ при его перемещении из т. $$ K$$ в бесконечность. Эта работа не изменится, если весь заряд $$ Q$$ сферы поместить в  центр сферы, т. к. поля обоих зарядов $$ Q$$ при $$ r>R$$ совпадают (см. §3). Для  точечного заряда $$ Q$$ отношение $$ {A}_{K\infty }/q$$ есть потенциал его поля в т. $$ K$$,  который находится по формуле (6.1). Итак, для сферы $$ {\varphi }_{K}=kQ/r$$. В предельном случае при $$ r=R$$ получим потенциал сферы, равный `kQ//R`.

Для произвольной точки $$ B$$ внутри сферы  $$ {\varphi }_{B}={A}_{BC\infty }/q={A}_{BC}+{A}_{C\infty }/q$$.

Здесь $$ {A}_{B\infty }$$, $$ {A}_{BC}$$ и $$ {A}_{C\infty }$$ – работа сил поля над зарядом $$ q$$ на участках $$ BC\infty $$,  `BC` и $$ C\infty .$$ Внутри сферы поля нет, сила на $$ q$$ со стороны поля не действует и $$ {A}_{BC}=0$$. Тогда $$ {\varphi }_{B}={A}_{C\infty }/q$$. Но правая часть последнего равенства есть потенциал т. $$ C$$, т. е. потенциал сферы, равный `kQ//R`. Значит, потенциал любой точки внутри сферы равен потенциалу сферы: $$ {\varphi }_{B}=kQ/R$$.

Итак, для заряда $$ Q$$, равномерно распределённого по сфере радиуса $$ R$$ потенциал поля вне сферы равен потенциалу точечного заряда, равного заряду сферы и помещённого в центре сферы (как и для напряжённости), а потенциал внутри сферы один и тот же и равен потенциалу сферы:

$$ \varphi =k{\displaystyle \frac{Q}{r}}$$ при $$  r>R, \varphi =k{\displaystyle \frac{Q}{R}}$$ при $$  r\le R$$.

Задача 6.1

В двух вершинах прямоугольника со сторонами $$ a$$ и $$ 2a$$ (рис. 6.2) закреплены точечные заряды $$ Q$$ и $$ 3Q$$. Какую минимальную работу надо совершить, чтобы переместить точечный заряд $$ 4Q$$ из состояния покоя из вершины $$ B$$ в вершину $$ C$$?

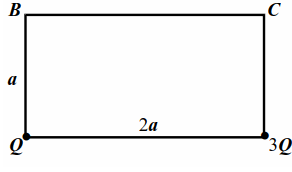Рис. 6.2


Решение

Здесь идёт речь о работе $$ A$$, которую необходимо совершить нам против электрических сил при переносе заряда $$ 4Q$$. Работа $$ A$$ в сумме с работой $$ {A}_{1}$$ сил электростатического поля над зарядом $$ 4Q$$ равна изменению кинетической энергии перемещаемого заряда:

$$ A+{A}_{1}=∆K$$

Отсюда $$ A=-{A}_{1}+∆K$$.

Работа $$ A$$ будет минимальной, если величина $$ ∆K$$ минимальна, т. е. заряд $$ 4Q$$ придёт в вершину $$ C$$ с нулевой скоростью, т. е. $$ ∆K=0.$$ Итак, $$ A=-{A}_{1}.$$ Работа сил поля над зарядом $$ {A}_{1}=4Q({\varphi }_{B}-{\varphi }_{C}), $$ где

$$ {\varphi }_{B}=k{\displaystyle \frac{Q}{a}}+k{\displaystyle \frac{3Q}{a\sqrt{5}}}, {\varphi }_{C}=k{\displaystyle \frac{Q}{a\sqrt{5}}}+k{\displaystyle \frac{3Q}{a}}$$

- потенциалы результирующего поля, созданного зарядами $$ Q$$ и $$ 3Q$$ в вершинах $$ B$$ и $$ C$$.

Окончательно 

$$ A={\displaystyle \frac{8(\sqrt{5}-1)}{\sqrt{5}}}{\displaystyle \frac{k{Q}^{2}}{a}}>0$$.

Задача 6.2

В центре сферы радиусом $$ R$$ находится точечный заряд $$ Q>0$$. По сфере равномерно распределён заряд $$-4Q<0$$. Найти потенциалы $$ {\varphi }_{A}, {\varphi }_{C}$$ на расстояниях $$ R/2$$ и $$ 2R$$ от центра сферы (рис. 6.3).

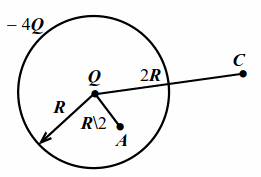Рис. 6.3


Решение

Потенциал в любой точке равен сумме потенциалов полей, созданных в этой точке зарядами $$ Q$$ и $$ -4Q$$. Для точек $$ A$$ и $$ C$$ :

$$ {\varphi }_{A}=k{\displaystyle \frac{Q}{R/2}}+k{\displaystyle \frac{-4Q}{R}}=-2k{\displaystyle \frac{Q}{R}}$$,

$$ {\varphi }_{C}=k{\displaystyle \frac{Q}{2R}}+k{\displaystyle \frac{-4Q}{2R}}=-{\displaystyle \frac{3}{2}}k{\displaystyle \frac{Q}{R}}$$.