 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
Самый простой способ создать равномерное распределение заряда по сферической поверхности – это зарядить проводящий шарик и уединить его. Заряд, в силу равноправности всех направлений из центра шарика, распределится по поверхности равномерно.
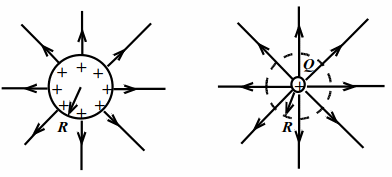
Сравним поле искомого заряда `Q` на сфере радиуса `R` и поле точечного заряда, равного заряду сферы. На рис. 3.1 показаны картины силовых линий полей этих зарядов для случая `Q > 0`.
 |
| Рис. 3.1 |
Число силовых линий, выходящих из зарядов сферы и точечного заряда, одинаково, т. к. заряды равны (свойство 3 предыдущего параграфа). Это означает, что картины силовых линий обоих полей (а значит, и напряжённости) совпадают на расстояниях `r >R`, считая от центра сферы или от точечного заряда. Внутри сферы силовых линий нет, нет и поля. В противном случае силовые линии, начавшись на сфере, могли бы идти в силу симметрии только к центру сферы. Но в центре нет заряда, на котором они могли бы закончиться. Итак,
вне сферы напряжённость поля заряда `Q`, равномерно распределённого по сферической поверхности (сфере) радиуса `R`, совпадает с напряжённостью поля точечного заряда, равного заряду сферы и помещённого в центре сферы, а внутри сферы поля нет:
$$ E=k{\displaystyle \frac{\left|Q\right|}{{r}^{2}}}$$ при $$ r>R, E=0$$ при `r<R`.
Здесь `r` – расстояние от центра сферы. Для записи выражения напряжённости вне сферы можно применить и формулу (2.3).
Говорить о напряжённости поля при `r=R` нет смысла, т. к. в рамках теории, когда не рассматриваются размеры конкретных носителей заряда на атомном уровне, напряжённость при `r = R` не определена.
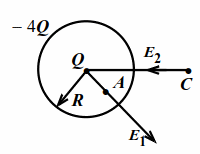
В центре сферы радиусом `R` находится точечный заряд `Q>0`. По сфере распределён равномерно заряд `-4Q<0`. Найти напряжённости $$ {E}_{1}, {E}_{2}$$ на расстояниях `R//2` и `2R` от центра сферы.
 |
| Рис. 3.2 |
В любой точке напряжённость равна векторной сумме напряжённостей полей, созданных зарядами `Q` и `-4Q`:
$$ \overrightarrow{E}=\overrightarrow{{E}_{Q}}+{\overrightarrow{E}}_{-4Q}.$$
Это векторное равенство можно записать в проекциях на ось `x`, проведённую из центра сферы через исследуемую точку: $$ {E}_{x}={E}_{Qx}+{E}_{-4Qx}.$$
Для точек `A` и `C` (рис. 3.2) на расстояниях `R//2` и `2R` от центра сферы проекция напряжённости на ось `x` (свою для каждой точки): $$ {E}_{2x}=k{\displaystyle \frac{Q}{{\left(2R\right)}^{2}}}+k{\displaystyle \frac{-4Q}{{\left(2R\right)}^{2}}}=-{\displaystyle \frac{3}{4}}k{\displaystyle \frac{Q}{{R}^{2}}}.$$
$$ {E}_{1}=\left|{E}_{1x}\right|=4k{\displaystyle \frac{Q}{{R}^{2}}}$$, напряженность направлена от центра сферы.
$$ {E}_{2}=\left|{E}_{2x}\right|={\displaystyle \frac{3}{4}}k{\displaystyle \frac{Q}{{R}^{2}}}$$, напряженность направлена к центру сферы.