 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
Опытным путём установлен закон Кулона:
сила взаимодействия двух точечных неподвижных зарядов в вакууме пропорциональна произведению модулей зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой, проходящей через эти заряды:
$$ F=k{\displaystyle \frac{\left|{q}_{1}\right|\left|{q}_{2}\right|}{{r}^{2}}} $$. (2.1)
Здесь `F` - модуль силы, `k` - коэффициент пропорциональности, зависящий от выбора системы единиц, `q_1` и `q_2` - величины зарядов, `r` - расстояние между зарядами.
Обратите внимание, что нарушение в конкретных условиях опыта точечности зарядов, их неподвижности или нахождение зарядов не в вакууме может привести к невыполнению соотношения (2.1).
Основной единицей в любой системе единиц называется единица, для которой существует установленная по договорённости принципиальная возможность создания эталона этой единицы. Напомним, что основными единицами системы СИ являются единицы длины метр (м), массы килограмм (кг), времени секунда (с), силы электрического тока ампер (А), термодинамической температуры кельвин (К), количества вещества моль (моль), силы света кандела (кд). Остальные единицы в системе СИ производные, их размерность (выраженная через основные или другие единицы системы) даётся через определения и физические законы, устанавливающие связь между различными физическими величинами. Единицей заряда в системе СИ является кулон (Кл) – заряд, проходящий за `1` с через поперечное сечение проводника при силе тока `1` А.
Найдём размерность (обозначается квадратными скобками) коэффициента `k` в формуле (2.1) закона Кулона. Для размерностей физических величин в (2.1) выполняется соотношение, аналогичное соотношению (2.1) между самими величинами: $$ \left[F\right]=\left[k\right]{\displaystyle \frac{\left[{q}_{1}\right]\left[{q}_{2}\right]}{\left[{r}^{2}\right]}}$$.
Поскольку $$ \left[F\right]=H=\mathrm{кг}·\mathrm{м}/{\mathrm{с}}^{2}, \left[{q}_{1}\right]=\left[{q}_{2}\right]=\mathrm{Кл}=\mathrm{А}·\mathrm{с}, \left[{r}^{2}\right]={\mathrm{м}}^{2}$$, то
$$ \left[k\right]={\displaystyle \frac{\left[F\right]\left[{r}^{2}\right]}{\left[{q}_{1}\right]\left[{q}_{2}\right]}}={\displaystyle \frac{\mathrm{Н}·{\mathrm{м}}^{2}}{{\mathrm{Кл}}^{2}}}={\displaystyle \frac{\mathrm{кг}·{\mathrm{м}}^{3}}{{\mathrm{А}}^{2}·{\mathrm{с}}^{4}}}$$.
Запоминать выражение для размерности `k` необязательно, но уметь выводить, используя (2.1), надо.
Приведём значение коэффициента `k` в (2.1) для системы СИ:
$$ k=9·{10}^{9}{\displaystyle \frac{\mathrm{кг}·{\mathrm{м}}^{3}}{{\mathrm{А}}^{2}·{\mathrm{с}}^{4}}}=9·{10}^{9} \mathrm{ед}. \mathrm{СИ}$$.
Заметим, что вместо выражения для размерности после численного значения можно писать «ед. СИ» (единицы СИ). Иногда в системе СИ коэффициент `k` в (2.1) записывают в форме $$ k={\displaystyle \frac{1}{4\pi {\epsilon }_{0}}}$$.
Здесь $$ {\epsilon }_{0}=\mathrm{8,85}·{10}^{-12}$$ ед. СИ называется электрической постоянной.
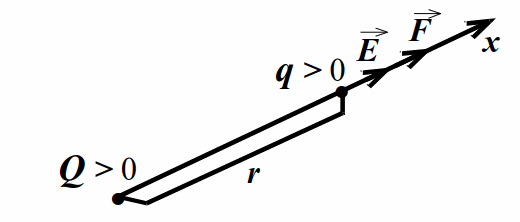
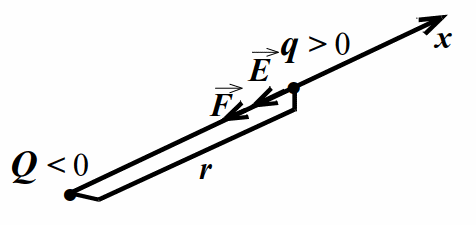
Найдём напряжённость электрического поля, созданного точечным зарядом `Q` на расстоянии `r` от заряда. Для этого поместим мысленно на расстоянии `r` от `Q` пробный заряд `q`. По закону Кулона на `q` действует сила $$ F=\left|\overrightarrow{F}\right|=k\left|Q\right|\left|q\right|/{r}^{2}$$. Напряжённость поля (созданного зарядом `Q`) в месте расположения `q` равна `vecE=vecF//q`. Отсюда `E=|vecE|=|vecF|//|q|`. С учётом выражения для `F` напряженность поля точечного заряда `Q` на расстоянии `r` от него
$$ E=k{\displaystyle \frac{\left|Q\right|}{{r}^{2}}}$$. (2.2)
 |
 |
| Рис. 2.1 | Рис. 2.2 |
На рисунках 2.1 и 2.2 показаны случаи для `Q > 0` и `Q < 0`. Знак пробного заряда `q` выбран положительным из соображений удобства, т. к. при таком выборе направление силы, действующей на `q`, совпадает с направлением напряжённости.
Формулу (2.2) можно обобщить, избавившись от знака модуля:
$$ {E}_{x}=k{\displaystyle \frac{Q}{{r}^{2}}}$$ (2.3)
Здесь $$ {E}_{x}$$ – проекция напряжённости на ось `x`, направленную от заряда `Q` и проходящую через исследуемую точку. Справедливость (2.3) при любом знаке `Q` проверяется непосредственно (см. рис. 2.1, 2.2).
Силовой линией (линией напряжённости) электрического поля называется непрерывная линия, касательная в каждой точке которой совпадает с направлением вектора напряжённости электрического поля в этой точке.Наглядно электрические поля изображают с помощью силовых линий.
На рис. 2.3 приведена картина силовых линий электрического поля положительного точечного заряда.
 |
| Рис. 2.3 |
Стрелкой на каждой силовой линии указывается её направление, т. е. направление вектора напряжённости в каждой точке силовой линии. Полезно посмотреть и нарисовать самим картины силовых линий полей из школьного учебника.
Все свойства силовых линий как электрического поля, так и электростатического поля, следуют из определения силовых линий и из законов электродинамики. Приведём некоторые свойства.
1. Силовые линии электрического поля не пересекаются. В противном случае в точках пересечения была бы неопределённость в направлении напряжённости поля.
2. Густота силовых линий электрического поля в пространстве пропорциональна напряжённости электрического поля.
3. Силовые линии электростатического поля не замкнуты. Они начинаются на положительных зарядах (или в бесконечности) и заканчиваются на отрицательных зарядах (или в бесконечности). При этом некоторая группа силовых линий (лучевая трубка) связывает равные по модулю заряды и число силовых линий, выходящих (входящих) из заряженного тела, не зависит от формы тела, а зависит только от величины заряда (пропорционально заряду).
Обратите внимание, что первые два свойства справедливы и для электростатического поля, как частного случая электрического. Третье же свойство справедливо только для электростатического поля, а для произвольного электрического поля выполняется не всегда.
 |
| Рис. 2.4 |
В двух вершинах равностороннего треугольника со стороной `a=1` м расположены точечные заряды $$ {q}_{1}=Q=1.4·{10}^{-7}\mathrm{Кл}$$, $$ {q}_{2}=-2Q$$. Найти напряжённость (модуль) электрического поля в третьей вершине треугольника.
Пусть напряженность полей, созданных зарядами `Q` и `-2Q` в третьей вершине треугольника $$ \overrightarrow{{E}_{1}}, \overrightarrow{{E}_{2}}$$ (рис. 2.4). По принципу суперпозиции полей напряжённость результирующего поля $$ \overrightarrow{E}=\overrightarrow{{E}_{1}}+\overrightarrow{{E}_{2}}.$$ Используя теорему косинусов для треугольника, составленного из векторов $$ \overrightarrow{E}, \overrightarrow{{E}_{1}}, \overrightarrow{{E}_{2}}$$, получаем $$ {E}^{2}={{E}^{2}}_{1}+{{E}^{2}}_{2}-2{E}_{1}{E}_{2}\mathrm{cos}60°. $$ Поскольку `E_1=kQ//a^2`, `E_2=2kQ//a^2`, `cos60^@=1//2`, то `E=sqrt3k Q/q^2~~2,2*10^3` Н/Кл.