В схеме на рис. 17.1 $$ {\mathcal{E}}_{1}=12$$ В, $$ {\mathcal{E}}_{2}=3$$ В, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.

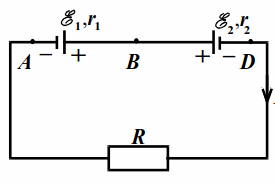Рис. 17.1

Найти напряжения на зажимах источников, т. е. разность потенциалов $$ {\varphi }_{A}-{\varphi }_{B}$$ и $$ {\varphi }_{B}-{\varphi }_{D}$$.

ЭДС батареи последовательно соединённых источников:

$$ \mathcal{E}={\mathcal{E}}_{1}-{\mathcal{E}}_{2}=9$$ B.

Причём, полярность батареи совпадает с полярностью источника $$ {\mathcal{E}}_{1}$$ т. к. $$ {\mathcal{E}}_{1}>{\mathcal{E}}_{2}$$.

Ток по закону Ома для замкнутой цепи $$ I=\mathcal{E}/(R+{r}_{1}+{r}_{2})=1$$ A. По закону Ома для участков цепи `AB` и `BD`:

$$ {\varphi }_{A}-{\varphi }_{B}+{\mathcal{E}}_{1}=I{r}_{1,}$$, $$ {\varphi }_{B}-{\varphi }_{D}-{\mathcal{E}}_{2}=I{r}_{2}$$.

Отсюда $$ {\varphi }_{A}-{\varphi }_{B}=I{r}_{1}-{\mathcal{E}}_{1}=-11$$ B, $$ {\varphi }_{B}-{\varphi }_{D}=I{r}_{2}+{\mathcal{E}}_{2}=5$$ B.

Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.

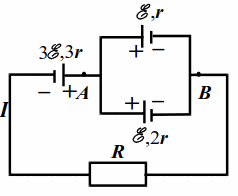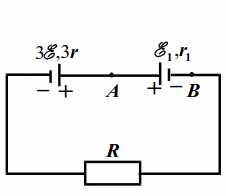Рис. 17.2	Рис. 17.3

Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ {\mathcal{E}}_{1}=\mathcal{E}$$, $$ {r}_{1}=r·2r/\left(r+2r\right)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3\mathcal{E}$$ и $$ {\mathcal{E}}_{1}$$:

$$ {\mathcal{E}}_{0}=3\mathcal{E}-{\mathcal{E}}_{1}=3\mathcal{E}-\mathcal{E}=2\mathcal{E}$$,

$$ {r}_{0}=3r+{r}_{1}=3r+2r/3=11r/3$$.

Ток $$ I={\displaystyle \frac{{\mathcal{E}}_{0}}{R+{r}_{0}}}={\displaystyle \frac{6\mathcal{E}}{3R+11r}}$$.