Автор
Чивилев Виктор Иванович 1229 статей

§ 16. Последовательное и параллельное соединение проводников

При последовательном соединении проводников с сопротивлениями $$ {R}_{1}, {R}_{2}, {R}_{3}, ...$$ ток $$ I  $$равен току в каждом:

$$ I={I}_{1}={I}_{2}={I}_{3}=...$$

На рис. 16.1 показано последовательное соединение двух проводников. Общая разность потенциалов (напряжение) всего участка цепи, как легко показать, равна сумме напряжений на отдельных проводниках:

Рис. 16.1


$$ U={U}_{1}+{U}_{2}+{U}_{3}+...$$

Можно вывести, что общее сопротивление при последовательном соединении проводников:

$$ R={R}_{1}+{R}_{2}+{R}_{3}+...$$

В частном случае последовательного соединения $$ n$$ проводников сопротивлением $$ {R}_{1}$$ каждый $$ R=n{R}_{1}$$.


$$ I={I}_{1}+{I}_{2}+{I}_{3}+...$$. При параллельном соединении проводников ток `I` равен сумме токов во всех проводниках:

На рис. 16.2 показано параллельное соединение двух проводников. Общее напряжение равно напряжению на каждом проводнике:

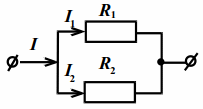Рис. 16.2

$$ U={U}_{1}={U}_{2}={U}_{3}=...$$

Можно показать, что общее сопротивление $$ R$$ при параллельном соединении проводников с сопротивлениями $$ {R}_{1}, {R}_{2}, ...$$ находится из равенства

$$ {\displaystyle \frac{1}{R}}={\displaystyle \frac{1}{{R}_{1}}}+{\displaystyle \frac{1}{{R}_{2}}}+...$$

В частном случае параллельного соединения двух проводников $$ R={\displaystyle \frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}}$$.

В другом частном случае параллельного соединения $$ n$$ проводников сопротивлением $$ {R}_{1}$$ каждый $$ R={R}_{1}/n$$.

Задача 16.1

В схеме на рис. 16.3 $$ {R}_{1}=1$$ Ом, $$ {R}_{2}=2$$ Ом, $$ {R}_{3}=6$$ Ом, $$ {R}_{4}=9$$ Ом, $$ {R}_{5}=5$$ Ом, $$ \mathcal{E}=12$$ В. $$ r=\mathrm{0,5}$$ Ом. Найти ток через резистор $$ {R}_{1}$$.

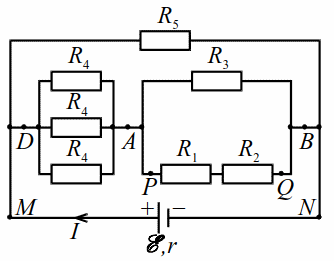Рис. 16.3


Решение

Задачи с громоздкими схемами удобно рассчитывать не в общем виде, а численно, т. е. последовательно находить численные значения параметров схемы. Расставим точки `A`, `B`, `D`, `M`, `N`, `P`, `Q` на схеме.

Сопротивление участка `PQ`   `R_(PQ)=R_1+R_2=3` Ом.

Сопротивление участка `AB`  $$ {R}_{AB}={\displaystyle \frac{{R}_{3}{R}_{PQ}}{{R}_{3}+{R}_{PQ}}}=2$$ Ом.

Сопротивление участков `DA`, `DB` и `MN` будут `R_(DA)=R_4//3=3` Oм, `R_(DB)=R_(DA)+R_(AB)=5` Ом, $$ {R}_{MN}={\displaystyle \frac{{R}_{DB}{R}_{5}}{{R}_{DB}+{R}_{5}}}=\mathrm{2,5}$$ Ом.

Заметим, что оказалось $$ {R}_{DB}={R}_{5}=5$$ Ом. Тогда можно было бы сразу написать $$ {R}_{MN}={\displaystyle \frac{{R}_{5}}{2}}=2,5$$ Ом.

По закону Ома для замкнутой цепи $$ I={\displaystyle \frac{\mathcal{E}}{{R}_{MN}+r}}=4$$ A.

Теперь пойдём «обратно», вычисляя параметры схемы и приближаясь к $$ {R}_{1}$$. Напряжение между точками $$ M$$ и `N` $$ {U}_{MN}=I{R}_{MN}=10$$ B.

Напряжение $$ {U}_{DB}={U}_{MN}=10$$ B.

Ток на участке `DB` `I_(DB)=U_(DB)//R_(DB)=2` A.

Напряжение $$ {U}_{AB}={I}_{DB}{R}_{AB}=4$$ B.

Так как $$ {U}_{AB}={U}_{PQ}$$, то ток через $$ {R}_{1}$$ составит: 

$$ {I}_{1}={I}_{PQ}={\displaystyle \frac{{U}_{PQ}}{{R}_{PQ}}}={\displaystyle \frac{{U}_{AB}}{{R}_{PQ}}}={\displaystyle \frac{4}{3}}$$ A.