 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
Пусть на свободные заряды участка цепи `1-2` действуют сторонние силы (силы неэлектростатического происхождения). Тогда говорят, что на участке `1-2` действует электродвижущая сила (ЭДС). За направление действия ЭДС будем считать направление действия сторонних сил на положительные заряды.
Для участка цепи `1-2` можно вывести, используя закон сохранения и превращения энергии, закон Ома для участка цепи, содержащего ЭДС:
| $$ \left(\varphi 1-\varphi 2\right)\pm \mathcal{E}=\pm IR$$. | (13.1) |
Здесь $$ \left({\varphi }_{1}-{\varphi }_{2}\right)$$- разность потенциалов (напряжение) между точками `1` и `2`, $$ \mathcal{E}$$ – ЭДС, действующая на участке `1-2`, $$ I$$ – сила тока, $$ R$$ – сопротивление участка `1-2`. В (13.1) величины $$ I$$ и $$ \mathcal{E}$$ взяты положительными, что удобно на практике. При этом справедливо правило знаков: перед $$ \mathcal{E}$$ (или $$ I$$ ) берётся знак `«+»`, если направление действия ЭДС (или направление тока) совпадает с направлением от `1` к `2` и наоборот. Величина $$ IR$$ называется падением напряжения.
На схемах ЭДС на участках цепи обозначается 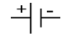 , наличие у участка цепи сопротивления обозначается.
, наличие у участка цепи сопротивления обозначается.  . Причём ЭДС и сопротивление могут быть «размазаны» по участку `1-2` произвольным образом и поэтому порядок расположения этих двух символических обозначений для участка цепи в схеме не играет роли. Направление действия ЭДС совпадает с направлением от `«-»` к `«+»` на символическом обозначении.
. Причём ЭДС и сопротивление могут быть «размазаны» по участку `1-2` произвольным образом и поэтому порядок расположения этих двух символических обозначений для участка цепи в схеме не играет роли. Направление действия ЭДС совпадает с направлением от `«-»` к `«+»` на символическом обозначении.
Следует отметить, что равенство (13.1) справедливо не только для постоянных по времени, $$ I$$, $$ \mathcal{E}$$, $$ R$$ но и для их мгновенных значений.
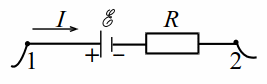 |
| Рис. 13.1 |
На участке цепи `1–2`, имеющем сопротивление $$ R=5$$ Ом, идёт ток $$ I=2$$ А и действует ЭДС $$ \mathcal{E}=12$$ В. Найти на участке `1–2` (рис. 13.1) падение напряжения и напряжение.
Падение напряжения есть $$ IR=10$$ B. По закону Ома для участка цепи, содержащего ЭДС, $$ \left({\varphi }_{1}-{\varphi }_{2}\right)-\mathcal{E}=IR$$. Отсюда напряжение
$$ {U}_{12}={\varphi }_{1}-{\varphi }_{2}=IR+\mathcal{E}=22$$ B.