$$ C={C}_{1}+{C}_{2}+...$$

Рис. 10.1

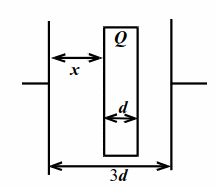
В плоский конденсатор параллельно его обкладкам вставлена пластина из диэлектрика с диэлектрической проницаемостью $$ \varepsilon $$ (рис. 10.1). Площадь обкладок конденсатора и пластины $$ S$$, толщина пластины $$ d$$, расстояние между обкладками $$ 3d$$. Найти ёмкость такого конденсатора.

Пусть расстояние от пластины до левой обкладки конденсатора $$ x$$. Наклеим мысленно на обе стороны пластины тонкую проводящую и незаряженную фольгу. От этого ничего не изменится. Обе фольги можно рассматривать как своеобразные провода, соединяющие три последовательно соединённых конденсатора с расстояниями $$ x$$, $$ d$$ и $$ 2d-x$$. Для общей ёмкости $$ C$$:

$$ {\displaystyle \frac{1}{C}}={\displaystyle \frac{x}{{\varepsilon }_{0}S}}+{\displaystyle \frac{d}{\varepsilon {\varepsilon }_{0}S}}+{\displaystyle \frac{2d-x}{{\varepsilon }_{0}S}}$$.

Окончательно $$ C={\displaystyle \frac{\varepsilon {\varepsilon }_{0}S}{d(2\varepsilon +1)}}.$$ Заметим, что не заданная в условии величина $$ x$$ «исчезла» в процессе решения.

Рис. 10.2

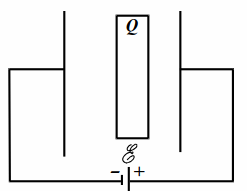
В плоский конденсатор ёмкостью $$ C$$ вставлена параллельно обкладкам плоская проводящая пластина с зарядом $$ Q$$ (рис. 10.2). Конденсатор подсоединён к источнику с ЭДС $$ \mathcal{E}$$. Площади пластины и обкладок конденсатора равны. Толщина пластины равна расстоянию от неё до правой обкладки и составляет четверть от расстояния между обкладками. Найти заряд конденсатора.

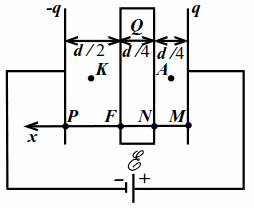
Пусть $$ d$$ – расстояние между обкладками, $$ S$$ – их площадь. Пусть $$ q$$ заряд правой обкладки. Тогда заряд левой будет $$ -q$$, т. к. заряд в значительных количествах не может накапливаться на соединительных проводах и в источнике. Направим ось $$ x$$ влево (рис. 10.3).

Рис. 10.3

Заметим, что поле внутри пластины отсутствует и разность потенциалов $$ {\varphi }_{N}-{\varphi }_{F}$$ между точками $$ N$$ и $$ F$$ равна нулю. Кроме того, заряды на поверхностях пластины создают вне пластины такое же поле, как и заряд $$ Q$$, если бы его расположить на любой из двух поверхностей пластины. Это легко показать отдельно.

Разность потенциалов $$ {\varphi }_{M}-{\varphi }_{P}$$ между точками $$ M$$ и $$ P$$ равна $$ \mathcal{E}$$. Поэтому

$$ ({\varphi }_{M}-{\varphi }_{N})+({\varphi }_{N}-{\varphi }_{F})+({\varphi }_{F}-{\varphi }_{P})=\mathcal{E}$$.

У нас $$ {\varphi }_{M}-{\varphi }_{N}={E}_{A}{\displaystyle \frac{d}{4}}, {\varphi }_{N}-{\varphi }_{F}=0, {\varphi }_{F}-{\varphi }_{P}={E}_{K}{\displaystyle \frac{d}{2}}$$.

Здесь - $$ {E}_{A}$$ и $$ {E}_{K}$$ - проекции напряжённости результирующего поля на ось `x`. По принципу суперпозиции полей

$$ {E}_{A}={\displaystyle \frac{q}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{Q}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{-q}{2{\varepsilon }_{0}S}}={\displaystyle \frac{1}{2{\varepsilon }_{0}S}}\left(2q-Q\right)$$,

$$ {E}_{K}={\displaystyle \frac{q}{2{\varepsilon }_{0}S}}+{\displaystyle \frac{Q}{2{\varepsilon }_{0}S}}-{\displaystyle \frac{-q}{2{\varepsilon }_{0}S}}={\displaystyle \frac{1}{2{\varepsilon }_{0}S}}\left(2q+Q\right)$$.

Подставляя выражения для $$ {E}_{A}$$, $$ {E}_{K}$$ и разностей потенциалов в первое
уравнение, получим после упрощений $$ 6q+Q=8\mathcal{E}{\displaystyle \frac{{\varepsilon }_{0}S}{d}}$$.

Так как $$ {\displaystyle \frac{{\varepsilon }_{0}S}{d}}=C$$, то $$ q=(8C\mathcal{E}-Q)/6$$.

Следует заметить, что знак найденного заряда правой обкладки зависит от соотношения заданных в условии задачи величин.

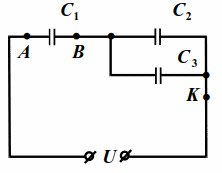Рис. 10.4

На схему (рис. 10.4) подано напряжение `U=24` В. Ёмкости конденсаторов `C_1=1` мкФ, $$ {C}_{2}=2$$ мкФ, $$ {C}_{3}=3$$ мкФ. Найти напряжения на конденсаторах.

В задачах, где есть схемы с конденсаторами, обычно предполагается, что схемы собраны из первоначально незаряженных конденсаторов.

Ёмкость между точками $$ B$$ и $$ K$$: 

$$ {C}_{BK}={C}_{2}+{C}_{3}=5$$ мкФ.

Общая емкость: $$ {C}_{AK}={\displaystyle \frac{{C}_{1}{C}_{BK}}{{C}_{1}+{C}_{BK}}}={\displaystyle \frac{5}{6}}$$ мкФ.

Общий заряд всей батареи конденсаторов $$ {q}_{AK}={C}_{AK}U=20·{10}^{-6 }\mathrm{Кл}.$$

Так как заряд $$ {q}_{1}$$ конденсатора $$ {C}_{1}$$ равен заряду батареи, то напряжение на этом конденсаторе $$ {U}_{1}={q}_{1}/{C}_{1}={q}_{AK}/{C}_{1}=20$$ В. Напряжения на конденсаторах $$ {C}_{2}$$ и $$ {C}_{3}$$ равны напряжению между точками $$ B$$ и $$ K$$ и в сумме с $$ {U}_{1}$$ дают $$ U$$.
Поэтому $$ {U}_{2}={U}_{3}={U}_{BK}=U-{U}_{1}=4$$ В.

Приведённая в задаче схема негромоздкая, и ответ легко получить в общем виде:

$$ {U}_{1}={\displaystyle \frac{{C}_{2}+{C}_{3}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=20$$ B,

$$ U2=U3={\displaystyle \frac{{C}_{1}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=4$$ B.