 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
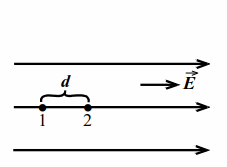
Пусть имеется однородное электростатическое поле с напряжённостью $$ E$$ (рис. 7.1). Возьмём точки `1` и `2` на силовой линии на расстоянии $$ d$$ друг от друга так, чтобы направление `1-2` совпадало с направлением силовой линии. Можно показать, что разность потенциалов (напряжение) $$ {\varphi }_{1}-{\varphi }_{2}$$ между точками `1` и `2`, напряжённость поля $$ E$$ и расстояние $$ d$$ связаны уравнением
| $$ {\varphi }_{1}-{\varphi }_{2}=Ed$$. | (7.1) |
 |
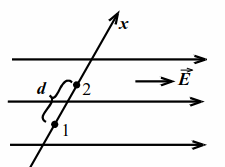 |
| Рис. 7.1 | Рис. 7.2 |
Зависимость (7.1) можно обобщить. Пусть в однородном поле есть произвольные точки `1` и `2` (рис. 7.2). Проведём через эти точки в направлении `1-2` ось $$ x$$. Можно показать, что
$$ {\varphi }_{1}-{\varphi }_{2}={E}_{x}d$$,
где $$ {E}_{x}$$ – проекция напряжённости поля на ось $$ x$$.
Соотношение (7.2) можно применить и для неоднородного поля, если только $$ d$$ настолько мало, что поле в окрестности точек `1` и `2` можно считать однородным.
Проанализировав (7.1), можно заключить, что потенциал убывает в направлении силовой линии поля. Это утверждение справедливо и для неоднородного поля.