 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
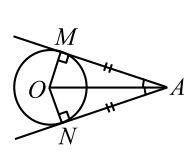 |
| Рис. 17 |
Если из точки к окружности проведены две касательные, то длины отрезков от этой точки до точек касания равны и прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам (рис. 17).
Используя это свойство, легко решить следующую задачу.
На основании $$ AC$$ равнобедренного треугольника $$ ABC$$ расположена точка $$ D$$ так, что $$ AD=a,CD=b$$. Окружности, вписанные в треугольники $$ ABD$$ и $$ DBC$$, касаются прямой $$ BD$$ в точках $$ M$$ и $$ N$$ соответственно. Найти отрезок $$ MN$$.
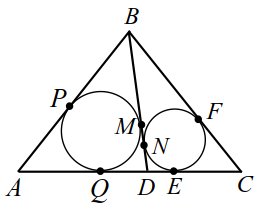 |
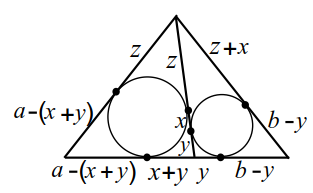 |
| Рис. 18 | Рис. 18a |
Пусть $$ a>b.$$ Точки касания окружностей со сторонами треугольника $$ ABC$$ обозначим и $$ F$$ (рис. 18). Положим По свойству касательных:
$$ DE=y$$, $$ QD=x+y$$, $$ AQ=AP=a-(x+y)$$, $$ EC=CF=b-y$$, $$ PB=BM=z, BF=BN=z+x$$ (рис. 18а). Выразим боковые стороны:
$$ AB=z+a-x-y$$, $$ BC=z+x+b-y$$. По условию $$ AB=BC$$; получим
$$ z+a-x-y=z+x+b-y$$, откуда находим $$ x={\displaystyle \frac{a-b}{2}}$$.
Если $$ a
Итак: $$ MN={\displaystyle \frac{\left|a-b\right|}{2}}.$$
Четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противолежащих сторон равны.
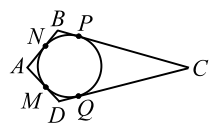 |
| Рис. 19 |
Пусть четырёхугольник $$ ABCD$$ описан около окружности (рис. 19).
По свойству касательных: $$ AM=AN$$, $$ NB=BP$$, $$ PC=CQ$$ и $$ QD=DM$$, поэтому
$$ AM+MD+BP+PC=AN+NB+CQ+QD$$, что означает
$$ AD+BC=AB+CD$$.
Докажем обратное утверждение. Пусть в выпуклом четырёхугольнике $$ ABCD$$ стороны удовлетворяют условию $$ AB+CD=BC+AD.$$ Положим $$ AD=a, AB=b, BC=c, CD=d.$$
По условию $$ a+c=b+d,$$ что равносильно $$ c-b=d-a.$$
Пусть $$ d>a.$$ Отложим на большей стороне $$ CD$$ меньшую сторону `DM=a` (рис. 20). Так как в этом случае $$ c>b$$, то также отложим $$ BN=b$$, получим три равнобедренных треугольника `ABN`, `ADM` и `MCN`.
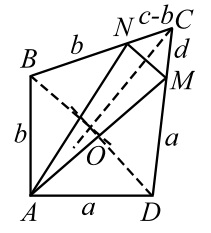 |
| Рис. 20 |
В равнобедренном треугольнике биссектриса угла при вершине является медианой и высотой, отсюда следует, что если провести биссектрисы углов `B`, `C` и `D`, то они разделят пополам соответственно отрезки `AN`, `MN` и `AM` и будут им перпендикулярны. Это означает, что биссектрисы будут серединными перпендикулярами трёх сторон треугольника $$ ANM$$, а они по теореме пересекаются в одной точке. Обозначим эту точку $$ O$$. Эта точка одинаково удалена от отрезков `AB` и `BC` (лежит на $$ OB$$), `BC` и `CD` (лежит на $$ OC$$) и `CD` и `AD` (лежит на $$ OD$$), следовательно, точка $$ O$$ одинакова удалена от всех четырёх сторон четырёхугольника $$ ABCD$$ и является центром вписанной окружности. Случай $$ d=a$$, как более простой, рассмотрите самостоятельно.
Равнобокая трапеция описана около окружности. Найти радиус окружности, если длины оснований равны $$ a$$ и $$ b$$.
 |
| Рис. 21 |
Пусть в равнобокой трапеции $$ ABCD$$ `BC=b`, `AD=a` (рис. 21). Эта трапеция равнобокая $$ (AB=CD)$$, она описана около окружности, следовательно, $$ AB+CD=AD+BC$$ Отсюда получаем:
$$ AB=CD={\displaystyle \frac{a+b}{2}}.$$
Проведём $$ BM$$ и $$ CN$$ перпендикулярно $$ AD$$. Трапеция равнобокая, углы при основании равны, следовательно, равны и треугольники $$ ABM$$ и $$ DCN$$ и $$ AM=ND$$. По построению $$ MBCN$$ - прямоугольник, $$ MN=BC=b$$ поэтому $$ AM={\displaystyle \frac{1}{2}}(AD-BC)-{\displaystyle \frac{1}{2}}(a-b)$$. Из прямоугольного треугольника $$ ABM$$ находим высоту трапеции $$ ABCD$$:
$$ BM=\sqrt{A{B}^{2}-A{M}^{2}}=\sqrt{{\left({\displaystyle \frac{a+b}{2}}\right)}^{2}-{\left({\displaystyle \frac{a-b}{2}}\right)}^{2}}=\sqrt{ab}$$.
Очевидно, что высота трапеции равна диаметру окружности, поэтому
радиус вписанной окружности равен $$ \overline{)r={\displaystyle \frac{1}{2}}\sqrt{ab}}$$.
Очень полезная задача. Заметим, что из решения также следует, что в равнобокой описанной трапеции $$ \overline{)\mathrm{cos}\alpha ={\displaystyle \frac{a-b}{a+b}}}$$.
Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключённой между его сторонами (рис. 22).
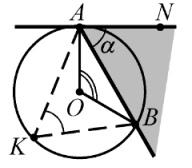 |
| Рис. 22 |
Рассматриваем угол $$ NAB$$ между касательной $$ NA$$ и хордой $$ AB$$. Если $$ O$$ - центр окружности, то $$ OA\perp AN$$, `/_OAB=/_OBA=90^@alpha`. Сумма углов треугольника равна `180^@`, следовательно, $$ \angle AOB=2\alpha $$. Итак, $$ \alpha =\angle NAB={\displaystyle \frac{1}{2}}\angle AOB.$$
Обратим внимание, что угол $$ NAB$$ равен любому вписанному углу $$ AKB$$, опирающемуся на ту же дугу $$ AB$$.
Случай `/_alpha>=90^@` рассматривается аналогично.
Из этого свойства следует важная теорема «о касательной и секущей», которая часто используется при решении задач.
Пусть к окружности проведены из одной точки касательная $$ MA$$ и секущая $$ MB$$, пересекающая окружность в точке $$ C$$ (рис. 23). Тогда справедливо равенство
$$ M{A}^{2}=MB·MC$$
т. е. если из точки `M` к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки `M` до точки касания равен произведению длин отрезков секущей от точки `M` до точек её пересечения с окружностью.
Угол $$ MAC$$ образован хордой и касательной, $$ \angle MAC=\angle ABC$$. Так как в треугольниках $$ MAC$$ и $$ MBA$$ угол $$ M$$ общий, то по двум углам они подобны. Из подобия следует:
$$ {\displaystyle \frac{MA}{MB}}={\displaystyle \frac{MC}{MA}}$$
Откуда получаем: $$ M{A}^{2}=MB·MC$$.
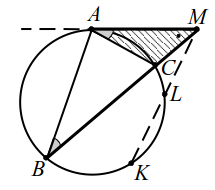 |
| Рис. 23 |
Если из точки $$ M$$ к окружности проведены две секущие: $$ MB$$, пересекающая окружность в точке $$ C$$ и $$ MK$$, пересекающая окружность в точке $$ L$$ (рис. 23), то справедливо равенство $$ MB·MC=MK·ML$$.
Проведём касательную $$ MA$$. По доказанной теореме $$ M{A}^{2}=MB·MC$$ и $$ M{A}^{2}=MK·ML$$, следовательно $$ MB·MC=MK·ML$$.
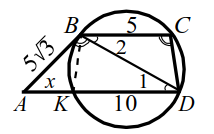 |
| Рис. 24 |
Окружность проходит через вершины $$ C u D$$ трапеции $$ ABCD,$$ касается боковой стороны $$ AB$$ в точке $$ B$$ и пересекает большее основание $$ AD$$ в точке $$ K$$ (рис. 24). Известно, что $$ AB=5\sqrt{3}$$, $$ BC=5$$ и $$ KD=10$$.
Найти радиус окружности.
1. Пусть $$ AK=x$$ тогда $$ AD=10+x$$ю
По теореме о касательной и секущей:
$$ A{B}^{2}=AK·KD$$ т. е. $$ 75=x(x+10)$$, откуда $$ x=5$$. Итак $$ AD=15$$.
2. Заметим теперь, что угол $$ ABD$$ между касательной $$ AB$$ и хордой $$ BD$$ равен вписанному углу $$ BCD$$, а из параллельности прямых $$ AD$$ и $$ BC$$ следует равенство углов `1` и `2`. По первому признаку подобия $$ △ABD\sim △DCB$$. Из подобия имеем $$ {\displaystyle \frac{AB}{CD}}={\displaystyle \frac{AD}{BD}}{\displaystyle \frac{BD}{BC}}$$. Из последнего равенства находим, что $$ B{D}^{2}=AD·BC$$, т. е. $$ BD=\sqrt{AD·BC}=5\sqrt{3}$$, а из первого равенства находим $$ CD={\displaystyle \frac{AB·BD}{AB}}=5$$.
3. Так как $$ KB=CD$$ ($$ KBCD$$ - вписанная трапеция, она равнобокая), и $$ K{B}^{2}+B{D}^{2}=K{D}^{2},$$ то `/_ KBD=90^@` и $$ KD$$ - диаметр окружности.
Значит, её радиус равен `5`.
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противолежащих углов равна `180^@`.
Из этой теоремы следует:
a) из всех параллелограммов только около прямоугольника можно описать окружность;
б) около трапеции можно описать окружность только тогда, когда она равнобокая.
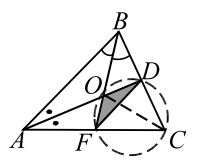 |
| Рис. 25 |
В треугольнике $$ ABC$$ биссектрисы $$ AD$$ и $$ BF$$ пересекаются в точке $$ O$$ (рис. 25). Известно, что точки $$ F, O, D$$, и `C` лежат на одной окружности и что $$ DF=\sqrt{3}.$$ Найти площадь треугольника $$ ODF$$.
Так как
$$ \angle BAO={\displaystyle \frac{1}{2}}\angle A$$ и $$ \angle ABO={\displaystyle \frac{1}{2}}\angle B$$, то
$$ \angle DOF=\angle AOB=\pi -{\displaystyle \frac{1}{2}}(\angle A+\angle B)$$.
Четырёхугольник $$ DOFC$$ вписан в окружность, по теореме 9:
$$ \angle DOF=\pi -\angle C$$, т. е. $$ \pi -{\displaystyle \frac{1}{2}}(\angle A+\angle B)=\pi -\angle C$$, откуда, учитывая, что $$ \angle A+\angle B+\angle C=\pi $$, находим $$ \angle С={\displaystyle \frac{\pi }{3}}$$.
Теперь заметим, что $$ O$$ - точка точка пересечения биссектрис, $$ CO$$ - биссектриса угла $$ C,$$ следовательно, углы $$ OCD$$ и $$ OCF$$ равны друг другу. Это вписанные углы, поэтому вписанные углы $$ ODF$$ и $$ OFD$$ равны им и равны друг другу. Таким образом,
$$ \angle ODF=\angle OFD={\displaystyle \frac{1}{2}}\angle C={\displaystyle \frac{\pi }{6}}$$.
Треугольник $$ DOF$$ равнобедренный с основанием $$ DF=\sqrt{3}$$ и углом при основании `30^@`. Находим его высоту, опущенную из вершины $$ O$$ и площадь треугольника $$ ODF: S={\displaystyle \frac{1}{2}}h·DF={\displaystyle \frac{\sqrt{3}}{4}}$$.