Два треугольника подобны:

• 1) если два угла одного соответственно равны двум углам другого;
• 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
• 3) если три стороны одного треугольника пропорциональны трём сторонам другого.

1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

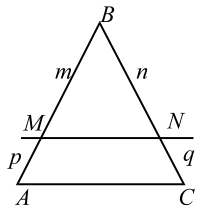Рис. 5

2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам,   т. е. если  $$ MN\left|\right|AC$$ (рис. 5), то

$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}=\frac{m+p}{n+q}$$

3°. Если  прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{m+p}{n+q}}$$ или $$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}$$,

то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для  9 класса).

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если  основания  трапеции равны $$ a$$ и $$ b$$.

Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.\;\left.\begin{array}{l}BC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm{по}\;\mathrm{двум}\;\mathrm{углам})\end{array}\right|\Rightarrow\dfrac ba=\dfrac pq$$                                        (1)

$$2.\;\left.\begin{array}{l}MO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right|\Rightarrow\dfrac xa=\dfrac p{p+q}$$.                                         (2)

Из (1) и (2) следует $$ x=a{\displaystyle \frac{p}{p+q}}=q{\displaystyle \frac{p/q}{p/q+1}}={\displaystyle \frac{ab}{a+b}}$$, т. е. $$ MO={\displaystyle \frac{ab}{a+b}}.$$

Аналогично устанавливаем, что $$ NO={\displaystyle \frac{ab}{a+b}}$$, поэтому $$ \overline{)MN={\displaystyle \frac{2ab}{a+b}}}$$.

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить. 

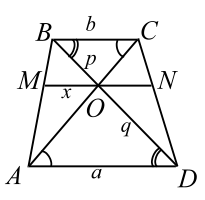Рис. 6

Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные  элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.

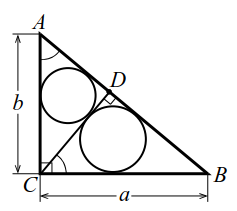Рис. 7

В прямоугольном треугольнике  $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы  окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ {r}_{1}$$ и $$ {r}_{2}$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.

 Обозначим искомый радиус $$ r$$, положим $$ AB=c$$, $$ AC=b$$, $$ BC=a$$. Из подобия прямоугольных треугольников $$ ACD$$ и $$ ABC$$ (у   них   равные углы при вершине $$ A$$) имеем $$ {\displaystyle \frac{r}{{r}_{1}}}={\displaystyle \frac{c}{b}}$$, откуда $$ b={\displaystyle \frac{{r}_{1}}{r}}c$$. Прямоугольные треугольники  $$ BCD$$ и  $$ BAC$$ также  подобны,  поэтому $$ {\displaystyle \frac{r}{{r}_{2}}}={\displaystyle \frac{c}{a}}$$, - откуда $$ a={\displaystyle \frac{{r}_{2}}{r}}c$$. Так как $$ {a}^{2}+{b}^{2}={c}^{2}$$ то, возводя в квадрат выражения для  $$ a$$ и $$ b$$ и складывая их, получим $$ {\left(\frac{{r}_{1}}{r}\right)}^{2}{c}^{2}+{\left(\frac{{r}_{2}}{r}\right)}^{2}{c}^{2}={c}^{2}$$ или $$ {\displaystyle \frac{{r}_{1}^{2}+{r}_{2}^{2}}{{r}^{2}}}=1$$.  Находим  $$ r=\sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}$$. 

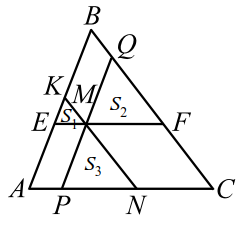Рис. 8

Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ {S}_{1}$$, $$ {S}_{2}$$  и $$ {S}_{3}$$. Найти  площадь треугольника $$ ABC$$.

Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.

Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда

$$ {\displaystyle \frac{{S}_{1}}{S}}={\left({\displaystyle \frac{EM}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{2}}{S}}={\left({\displaystyle \frac{MF}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{3}}{S}}={\left({\displaystyle \frac{PN}{AC}}\right)}^{2}.$$

Откуда находим

$$ EM=\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}AC, MF=\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}AC, PN=\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}AC.$$

А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.

Таким образом, $$ AC=AC·\left(\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}\right)$$, откуда следует

$$ S={\left(\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+\sqrt{{S}_{3}}\right)}^{2}$$.

Рис. 9

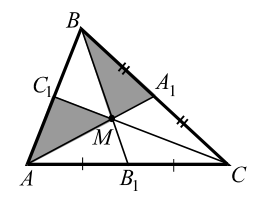
Теорема 1. Три медианы треугольника пересекаются в одной точке  и  точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ {\displaystyle \frac{1}{2}}{S}_{ABC}$$. Точка пересечения медиан называется центром тяжести треугольника. 

Теорема 3. Пусть $$ BD$$ - медиана треугольника 

$$ ABC (BC=a, AC=b, AB=c, BD={m}_{a})$$, тогда

$$ {m}_{c}^{2}={\displaystyle \frac{{a}^{2}+{b}^{2}}{2}}-{\displaystyle \frac{{c}^{2}}{4}}$$. (Доказательство приведено далее в §4 Задания).

Рис. 10

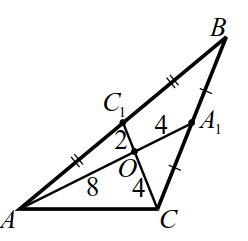
Медианы $$ A{A}_{1}$$ треугольника $$ ABC$$ пересекаются в точке $$ O$$, $$ A{A}_{1}=12$$ и $$ C{C}_{1}=6$$ и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника  $$ ABC$$.

1. По теореме 1 имеем  $$ AO={\displaystyle \frac{2}{3}}A{A}_{1}=8$$, $$ CO={\displaystyle \frac{2}{3}}C{C}_{1}=4$$. 

Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ - нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A{C}_{1}=6$$ и треугольник $$ AO{C}_{1}$$  со сторонами `8`, `2`, `6` не существует. Значит,  $$ BC=12$$ и $$ A{C}_{1}=6$$.

2. Площадь треугольника находим по формуле Герона:

$$ p=7, {S}_{{A}_{1}OC}=\sqrt{7·1·3·3}=3\sqrt{7}$$.

По теореме 2 площадь треугольника  $$ ABC$$ в `6` раз больше, находим $$ {S}_{ABC}=18\sqrt{7}$$.

Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Были доказаны также две леммы о высотах

1-ая лемма.

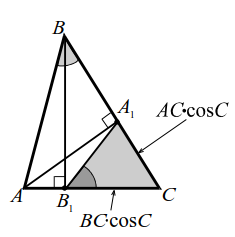
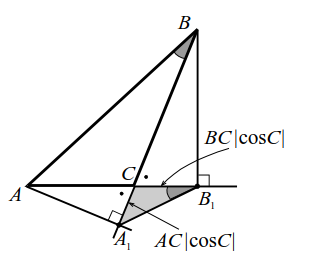
Если $$ A{A}_{1}$$ и $$ B{B}_{1}$$ - высоты треугольника $$ ABC$$, то треугольник $$ {A}_{1}{B}_{1}C$$ подобен треугольнику $$ ABC$$ с коэффициентом подобия $$ k={\displaystyle \frac{{A}_{1}{B}_{1}}{AB}}=\left|\mathrm{cos}C\right|$$. Можно это утверждение сформулировать так: Если соединить основания двух высот $$ A{A}_{1}$$ и $$ B{B}_{1}$$ треугольника $$ ABC$$, то образуется треугольник, подобный данному: $$ ∆{A}_{1}{B}_{1}C~∆ABC$$. 

Из прямоугольных треугольников $$ AC{A}_{1}$$ следует $$ {A}_{1}C=AC·\mathrm{cos}C$$ или $$ {A}_{1}C=AC·\mathrm{cos}(180°-C)=AC\left|\mathrm{cos}C\right|$$ (рис. 11а, б), а из прямоугольных треугольников $$ BC{B}_{1}$$ следует $$ {B}_{1}C=BC·\mathrm{cos}C$$ или $$ {B}_{1}C=BC·\mathrm{cos}(180°-C)=BC\left|\mathrm{cos}C\right|$$. Далее рассуждения очевидны.

Рис. 11a	Рис. 11б

2-ая лемма.

Если высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ (или их продолжения) пересекаются в точке $$ H$$, то справедливо равенство $$ AH·H{A}_{1}=BH·H{B}_{1}$$ (рис. 12а, б).

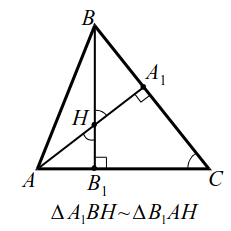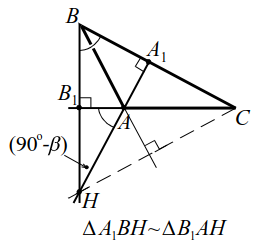Рис. 12a	Рис. 12б

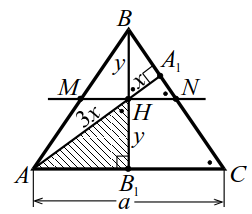Рис. 13

Высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ пересекаются в точке $$ H$$ (рис. 13), при этом $$ AH=3H{A}_{1}$$ и $$ BH=H{B}_{1}$$. Найти косинус угла $$ ACB$$ и площадь треугольника $$ ABC$$, если $$ AC=a$$.  

Обозначим $$ H{A}_{1}=x, H{B}_{1}=y$$, 

1. Точка $$ H$$ - середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен  основаниям,  то `MN` - средняя линия; `MN=a/2`.

2. $$\left.\triangle HA_1N\sim\triangle AA_1C\right|\Rightarrow\dfrac{HN}{AC}=\dfrac x{4x},\;HN=\dfrac14a.$$ Значит, $$ MH=HN={\displaystyle \frac{a}{4}}$$ и $$ A{B}_{1}={B}_{1}C={\displaystyle \frac{a}{2}}$$ Треугольник  $$ ABC$$  равнобедренный, $$ AB=BC$$.

3. $$ \angle {B}_{1}BC=90°-\angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах  $$ AH·H{A}_{1}=BH·H{B}_{1}$$ т. е.  $$ 3{x}^{2}={y}^{2}, y=x\sqrt{3}$$.

Далее, $$ \mathrm{cos}C=\mathrm{cos}(\angle AH{B}_{1})={\displaystyle \frac{y}{3x}}$$, находим $$ \mathrm{cos}C={\displaystyle \frac{1}{\sqrt{3}}}$$.

4. $$ △AH{B}_{1}: A{B}_{1}^{2}=(3x{)}^{2}-{y}^{2}$$, $$ {\displaystyle \frac{{a}^{2}}{4}}=6{x}^{2}$$, $$ x={\displaystyle \frac{a}{2\sqrt{6}}}$$, $$ y={\displaystyle \frac{a}{2\sqrt{2}}}$$, тогда

$$ {S}_{ABC}={\displaystyle \frac{1}{2}}AC·B{B}_{1}=ay={\displaystyle \frac{{a}^{2}\sqrt{2}}{4}}$$.

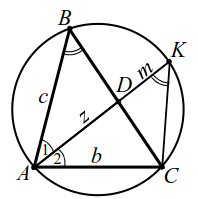
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим  сторонам, т. е.  если $$ AD$$ - биссектриса треугольника  $$ ABC$$ (рис. 14), то

$$ {\displaystyle \frac{BD}{DC}}={\displaystyle \frac{AB}{AC}} \left({\displaystyle \frac{x}{y}}={\displaystyle \frac{c}{b}}\right)$$

Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.

Теорема 6. Пусть $$ AD$$ - биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=\sqrt{AB·AC-DB·DC}$$ (в обозначениях рисунка 14а) 

`ul(AD=sqrt(bc-xy))`.

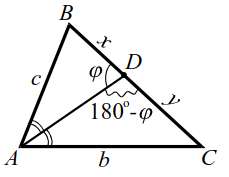Рис. 14			Рис. 14а

Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).

Обозначим  $$ AD=z, DK=m.△ABD\sim ∆AKC$$ $$ (\angle ABD=\angle AKC$$ и $$ \angle 1=\angle 2)$$. Из подобия следует $$ {\displaystyle \frac{AB}{AK}}={\displaystyle \frac{AD}{AC}}$$, т. е. $$ {\displaystyle \frac{c}{z+m}}={\displaystyle \frac{z}{b}}$$, откуда $$ {z}^{2}+zm=bc$$, $$ {z}^{2}=bc-zm$$.

По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ {z}^{2}=bc-xy$$, $$ z=\sqrt{bc-xy}$$.  

В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD={\displaystyle \frac{15}{8}}$$. Найти сторону $$ BC$$ и радиус вписанной окружности.

По теореме 5 (см. рис. 14) имеем $$ {\displaystyle \frac{x}{y}}={\displaystyle \frac{5}{3}}$$ Обозначим $$ x=5z$$, тогда  $$ y=3z$$. По теореме 6 выполнено равенство $$ {\left({\displaystyle \frac{15}{8}}\right)}^{2}=5·3-5z·3z.$$ Легко находим $$ z={\displaystyle \frac{7}{8}}$$ значит `ul(BC=7)`. Радиус вписанной окружности найдём по формуле $$ S=pr$$ (`S` - площадь треугольника,  `p` -полупериметр). Имеем $$ p={\displaystyle \frac{15}{2}}$$, по формуле Герона $$ S=\sqrt{{\displaystyle \frac{15}{2}}·{\displaystyle \frac{1}{2}}·{\displaystyle \frac{10}{2}}·{\displaystyle \frac{9}{2}}}={\displaystyle \frac{15\sqrt{3}}{2}},$$ поэтому $$ r={\displaystyle \frac{S}{p}}={\displaystyle \frac{\sqrt{3}}{2}}.$$