Основное внимание, как во всех Заданиях, уделяется методам и приёмам решения задач. Именно решение задач делает изучение вообще, и геометрии в частности, активным. Ведь каждая решённая задача - это некоторый поиск и, пусть небольшое, но открытие. «То, что вы были принуждены открыть сами, оставляет в вашем уме дорожку, которой вы сможете воспользоваться, когда в том возникнет необходимость» (это слова немецкого физика XVII столетия Лихтенберга, который известен своими афоризмами).

Итак, если хотите научиться решать задачи, приобрести навыки решения – учитесь этому, разбирайте решения в учебнике и нашем Задании, повторяйте эти решения (ведь так учатся всему), а затем пробуйте свои силы. У Вас получится.

Задание состоит из четырёх параграфов. В параграфе 1 повторяются признаки подобия треугольников, решается несколько характерных задач на эту тему, повторяются свойства медиан, биссектрис и высот треугольника. Во втором параграфе обсуждаются «задачи в делении отрезка» и доказывается теорема Менелая. Третий параграф посвящён свойствам касательных, хорд, секущих, вписанных и описанных четырёхугольников. В параграфе 4 рассматривается применение теорем синусов и косинусов, разобраны задачи, решение которых требует применение тригонометрии. Почти все эти темы разбирались в заданиях по геометрии в 9 и 10 классах ЗФТШ, поэтому более простые утверждения здесь приводятся без доказательства. Тем, кто поступил в ЗФТШ в 11 класс, рекомендуется доказать эти утверждения самостоятельно, а те, кто учится в ЗФТШ не первый год, найдут много новых интересных задач, подробно решённых в 19 примерах.

Задание оканчивается контрольными вопросами и задачами для самостоятельного решения; они оценены по трудности в очках, которые указаны в скобках после номера. Знаком * «звёздочка» отмечены более трудные вопросы и задачи.

За правильный ответ и верное решение задачи ставится полное число очков, за недочёты и ошибки определённое число очков снимается.

Работу над заданием рекомендуется начать с внимательного чтения его и самостоятельного решения (после ознакомления) всех приведённых в нём задач. Ответы на контрольные вопросы следует давать подробные, со ссылками на соответствующие теоремы учебника или данного задания, с доказательствами своих ответов. В случае отрицательного ответа должен быть приведён опровергающий пример. Приведём примеры ответов на контрольные вопросы.

Вопрос 1

Можно ли утверждать, что треугольник равнобедренный, если его биссектриса является медианой?

Ответ

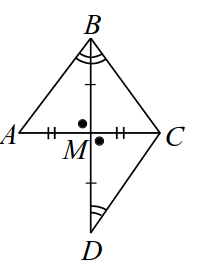Рис. 1

Да, можно. Докажем это. Пусть в треугольнике $ABC$ биссектриса `BM` является медианой: $AM=MC$ (рис. 1). На продолжении биссектрисы $BM$ отложим отрезок $MD$, равный $MB$. Треугольники $ABM$ и $CDM$ равны по первому признаку: у них углы при вершине $M$  равны как вертикальные и $AM=CM$, $BM=MD$. Из равенства треугольников следует

$CD=AB$                                   (1)

и $\angle CDM=\angle ABM$. Но $\angle ABM=\angle CBM$, поэтому $\angle CDM=\angle CBM$, т. е. в треугольнике $BCD$  углы при основании $BD$ равны. По теореме этот треугольник равнобедренный: $BC=CD$. Отсюда и из (1) заключаем: $BC=AB$. Утверждение доказано.

Вопрос 2

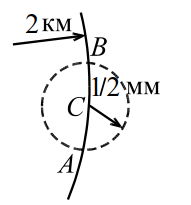Рис. 2

Могут ли длины сторон треугольника быть меньше `1` мм, а радиус описанной окружности больше `1` км?

ОТвет

Да, могут. Приведём пример. Из точки $C$, лежащей на окружности  радиуса `2` км, дугой радиуса $1/2$ мм отмечаем точки $A$ и $B$, лежащие на большей окружности (рис. 2); очевидно, $AC=CB=1/2$ мм.

Треугольник $ABC$ вписан в окружность радиуса `2` км, а его наибольшая сторона $AB$ < $AC+BC=1$ мм.

вопрос 3

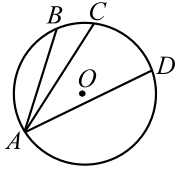Рис. 3

Можно ли через точку окружности провести три равные между собой хорды?

ответ

Нет, нельзя. Действительно, предположим противное, т. е. предположим, что хорды $AB$, $AC$ и $AD$ окружности с центром в точке $O$ равны между собой (рис. 3). Тогда точки $B$, $C$ и $D$ одинаково удалены от точки `A`, т. е. они лежат на окружности с центром в точке $A$. Однако, этого не может быть, так как две окружности с разными центрами не могут иметь более двух общих точек. Значит предположение неверно.

Вопрос 4

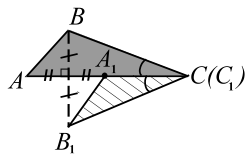Рис. 4

Верно ли, что $\triangle ABC=\triangle A_1B_1C_1$, если $AB=A_1B_1$, $BC=B_1C_1$, $\angle C=\angle C_1$?

Ответ

Нет, например, на рис. 4 показаны треугольники $ABC$ и $A_1B_1C_1$, для которых, как легко видеть, выполнены все заданные равенства, но $\triangle ABC\neq\triangle A_1B_1C_1$, так как $AC\neq A_1C_1$.

Итак, при утвердительном ответе надо либо привести доказательство того, что данное утверждение верно (как в ответе на вопрос 1), либо привести конкретный пример реализации заданных условий (как в ответе на вопрос 2).

При отрицательном ответе надо либо привести рассуждения, приводящие к противоречию заданных условий аксиоме, теореме или определению (как в ответе на вопрос 3), либо построить один опровергающий пример (как в ответе на вопрос 4).

После повторения тем в §1 – 4 в заключительном пятом параграфе обсудим вопросы подходов к решению, важность хорошего рисунка, выбора переменных, а также остановимся на некоторых ошибках, допускаемых учащимися и абитуриентами.

Это задание вместе с присланным решением будут Вам полезны при подготовке к экзаменам.