Примеры решения задач

Автор
Курносов Валерий Михайлович 326 статей

Примеры решения задач

Пример 1. Какие силы действуют на человека во время ходьбы? Какая сила приводит его в движение?

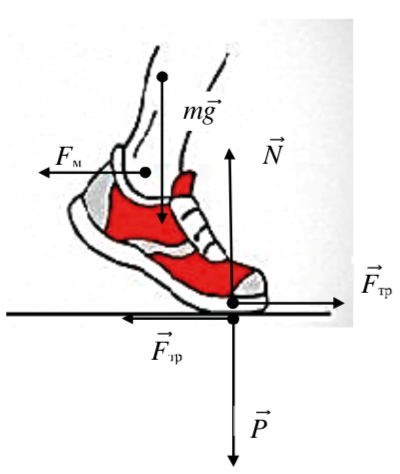Рис. 15

Решение: На человека всегда действует сила тяжести $(m\vec g)$ . Она приложена ко всем частям организма, но принято её изображать приложенной к центру масс (на рис. 15 это не так). Во время ходьбы человек мышечными усилиями толкает ногу назад, относительно центра масс (туловища). На рисунке эта сила обозначна как $\vec F_\mathrm{м}$ . Нога бы начала такое движение, если бы не было сцепления протектора подошвы и поверхности асфальта (пола). Вдоль поверхности возникает сила трения покоя. Нога толкает этой силой асфальт влево $(\vec F_\mathrm{тр})$ , а асфальт толкает ногу вправо $(\vec F_\mathrm{тр})$ , приводя её в движение относительно асфальта. Человек оказывает на поверхность асфальта действие, называемое весом $(\vec P)$ , а на человека действует противоположная сила реакции опоры $(\vec N)$ .

Пример 2. С каким ускорением будет двигаться тело массой $3\ \text{кг}$ по поверхности стола с коэффициентом трения $0,3$ , если к нему приложить силу $10\ \text{Н}$ под углом $30^\circ$ к горизонту?         

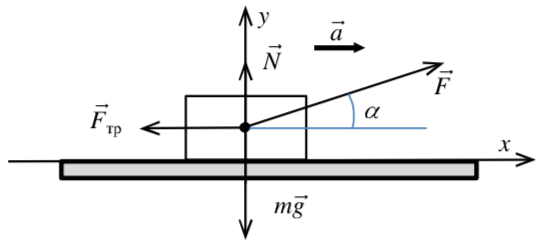Рис. 16

Решение. Расставим силы. При расстановке сил пользуются, преимущественно, двумя моделями: 1) все силы прикладывают к центру масс тела, который символизирует материальную точку, в качестве которой рассматривается тело; 2) точки приложения сил изображают там, где сила приложена. Во втором случае требуется применять ряд дополнительных правил, которые на первых порах излишне усложняют решение. На данном рисунке 16 применены правила первой модели.

Далее запишем 2-ой закон Ньютона в векторной форме:

$m\vec g + \vec F_\mathrm{тр} + \vec N + \vec F = m\vec a$ .

Теперь пишем проекции этого уравнения на оси $Ox$ и $Oy$ . Отметим, что оси удобнее всего выбирать из принципа удобства, что чаще всего соответствует направлению одной из осей вдоль ускорения, а второй оси перпендикулярно первой. Еcли движутся несколько тел, то для каждого тела можно выбирать свою удобную пару осей.

$Ox:\quad -F_\mathrm{тр} + F\cos \alpha = ma,$

$Oy:\quad -mg + N + F\sin \alpha = 0.$

Вспомогательное уравнение (формула Кулона – Амонтона):

$$F_\text{тр} =\mu \cdot N$$

Решая скалярную тройку уравнений, получим:

$a = \frac Fm (\mu\cdot \sin \alpha + \cos\alpha) - \mu g$ .

Подставим числовые значения и получим: $a\approx 0,39\ \frac{\text{м}}{\text{с}^2}$ .

При достаточной тренировке в решении задач запись в векторном виде становится излишней, и пишем сразу проекции на оси. На начальном этапе обучения пропускать эту запись не следует.         

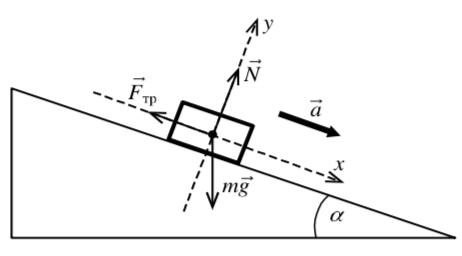Рис. 17

Пример 3. По наклонной плоскости с углом наклона при основании $\alpha = 30^\circ$ соскальзывает тело. Найти ускорение тела при коэффициенте трения поверхности и тела, равным $0,2$ .

Решение. На рисунке 17 расставим силы и выберем оси координат из принципа удобства (одна из осей вдоль ускорения).

Запишем уравнение второго закона Ньютона в векторном виде:

$m\vec g + \vec F_\mathrm{тр} + \vec N = m\vec a$ .

Далее проецируем его на оси координат:

$Ox:\quad -F_\mathrm{тр} + mg\cdot \sin \alpha = ma$ ,

$Oy:\quad -mg\cdot\cos\alpha + N = 0$

Добавим формулу Кулона-Амонтона:

$F_\mathrm{тр} = \mu\cdot N$ .

Решая систему уравнений, получим:

$a = g(\sin\alpha-\mu\cos\alpha)$ .

Числовой ответ даёт значение: $a\approx 3,27\ \frac{\text{м}}{\text{с}^2}$ .

Рассмотрим способ с другими направлениями осей (рис. 18) (неудобными)

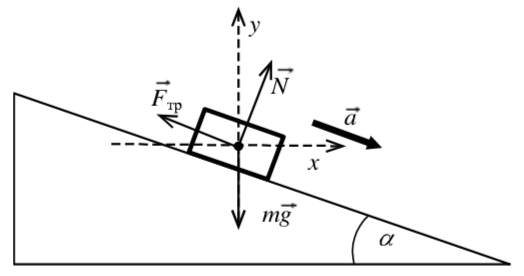
$Ox:\quad -F_\mathrm{тр}\cdot\cos\alpha + N\cdot\sin\alpha = ma\cdot\cos\alpha,$

$Oy:\quad -mg+N\cdot\cos\alpha = -a\cdot\sin\alpha$ .

Добавим формулу Кулона-Амонтона: $F_\mathrm{тр} = \mu\cdot N$ .

Решение этой системы уравнений так же приведёт к тому же ответу (проверьте самостоятельно), но путь достижения цели будет и длиннее, и сложнее.

Пример показывает рациональность предлагаемого принципа удобства.         

Рис. 19

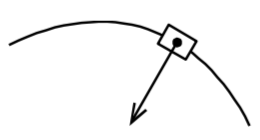
Пример 4. Коэффициент трения между резиной и асфальтом $0,7$ . Какой должна быть ширина дороги, чтобы на ней смог развернуться мотоциклист без уменьшения скорости, если его скорость равна $54\ \text{км}/\text{ч}$ ?

Если мотоциклист планирует развернуться, не уменьшая скорости, то движение его будет равномерным по окружности. Сила, приводящая к изменению направления скорости, будет сообщать центростремительное (нормальное) ускорение (рис. 19) . Этой силой будет сила трения.

Решение. Выберем ось $Ox$ вдоль ускорения (рис. 20) . Запишем 2-й закон Ньютона в проекции на эту ось:         

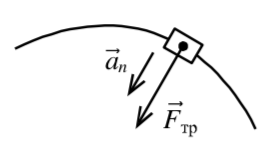Рис. 20

$F_\mathrm{тр} =ma_n = m\frac{v^2}{R}$ .

Так как $F_\mathrm{тр} = \mu N$ , а $N = mg$ , то $\mu mg = m\frac{v^2}{R}$ , откуда $R = \frac{v^2}{\mu g}$ , тогда для разворота нужна ширина:

$l = 2R;\quad l = \frac{2v^2}{\mu g};\quad l = 64,3\ \text{м}$

Из ответа видим, что для разворота на реальной дороге необходимо сниизить скорость.

Пример 5. Два тела массами $m_1 = 2\ \text{кг}, \ m_2 = 3\ \text{кг}$ связаны нитью. Первое тело тянут вправо с силой $F = 15\ \text{Н}$ по поверхности с коэффициентом трения $\mu = 0,1$ . Определите силу натяжения нити, связывающей тела. С каким ускорением движутся тела? Оборвётся ли нить, если поместить тела на поверхность с коэффициентом трения $0,3$ , а максимальная сила натяжения нити $10\ \text{Н}$ ?

Решение. Расставим силы, действующие на тела (рис. 21):

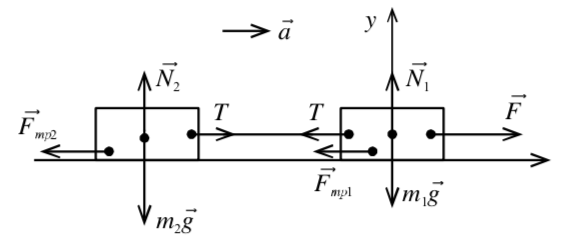
Рис. 21

Выберем ось $Ox$ вдоль силы $\vec F$ и ось $Oy$ перпендикулярно ей.

Второй закон Ньютона для двух тел в проекции на ось $Ox$ :

$F - F_\mathrm{тр1} - T + T - F_\mathrm{тр2} = (m_1 + m_2)a$ ,

для первого тела на ось $Oy$ :

$N_1 - m_1g = 0,\ \mathrm{тогда}\ F_\mathrm{тр1} = \mu m_1 g$ ;

для второго тела:

$N_2 - m_2g = 0 \Rightarrow \ F_\mathrm{тр2} = \mu m_2g$ .

Выразим ускорение из проекции $Ox$ , подставляя силы трения:

$a = \frac{F}{m_1 + m_2}-\mu g$ ,

$a = 2\ \frac{\text{м}}{\text{с}^2}$ .

Теперь запишем второй закон Ньютона для второго тела:

$Ox:\quad T-F_\mathrm{тр2} = m_2 a$ ,

откуда

$T = F_\mathrm{тр2} + m_2 a$ ,

$T = m_2(\mu g + a)$ ,

$T = \frac{m_2}{m_1 + m_2}F = 9\ \text{Н}$ .

Если $\mu = 0,3$ , то $a = 0$ , тела движутся равномерно, а сила натяжения нити останется прежней, $T = 9\ \text{Н} < 10\ \text{Н}$ . Нить не порвётся.

Пример 6. На вершине наклонной плоскости, с углом при основании $30^\circ$ укреплён неподвижный блок. Через блок перекинута невесомая и нерастяжимая нить . К нити привязаны два тела: $m_1 = 3\ \text{кг}$ со стороны плоскости и $m_2 = 4\ \text{кг}$ с другой. Коэффициент трения при движении тела по поверхности равен $0,2$ . Какова сила натяжения нити и ускорения тел?

Решение. Силы, действующие на тела, представлены на рисунке 22.

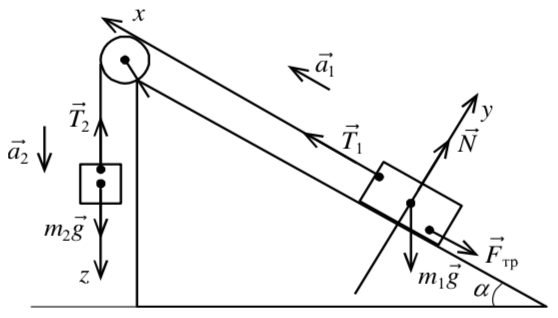
Рис. 22

Запишем 2-ой закон Ньютона для первого тела в проекциях:

$Ox:\quad T_1 - F_\mathrm{тр} - m_1 g\sin \alpha = m_1 a_1$ ,

$O_y:\quad N-m_1g\cos\alpha = 0$ .

С учётом, что $F_\mathrm{тр} = \mu N$ , получим $T_1 - \mu m_1 g\cos\alpha - m_1g\sin\alpha = m_1 a_1$ .

Для второго тела в проекции на $Oz$ :

$m_2g - T_2 = m_2a_2$ .

Решая совместно два уравнения, получим (учитывая, что $a_1 = a_2 = a$ и $T_1 = T_2 = T$ )

$a = \frac{m_2 - m_1\sin\alpha - \mu m_1\cos\alpha}{m_1 + m_2}g$ ,

$a \approx 2,83\ \text{м}/\text{с}^2$ .         

Рис. 23

Из этих же уравнения получим силу натяжения нити:

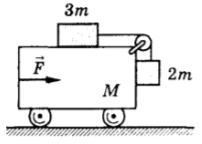
$T = g\frac{m_1m_2}{m_1 + m_2}(1 + \sin\alpha + \mu\cos\alpha)$

$T \approx 28,7\ \text{Н}$ .

Пример 7. Какую горизонтальную силу $F$ нужно приложить к тележке массой $M$ , чтобы бруски массой $2m$ и $3m$ (рис. 23) относительно неё не двигались? Трением пренебречь.

Решение. На рисунке 24 изображены силы, действующие на тела.

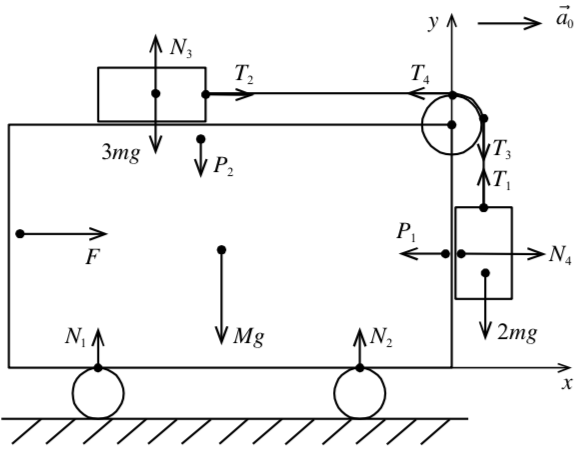
Рис. 24

Если трения нет и бруски неподвижны относительно тележки, то 2-й закон Ньютона в проекциях для тел примет вид:

1) для тележки:

$Ox:\quad F - P_1 - T_4 = Ma_0$ ,

$Oy:\quad N_1 + N_2 - Mg - P_2 - T_3 = 0$ ;

2) для бруска $3m$ :

$Ox:\quad T_2 = 3ma_2$ ,

$Oy:\quad N_3 - 3mg = 0,\quad N_3 = P_2$ ;

3) для бруска $2m$ :

$Ox:\quad N_4 = 2ma_1$ ,

$Oy:\quad T_1-2mg = 0, \quad N_4 = P_1$ ;

4) $T_1 = T_2 = T_3 = T_4\quad \text{(нить невесома)},$

5) $a_1 = a_2 = a_0\quad \mathrm{(нить}\ \mathrm{нерастяжима)}$

Решая совместно получим:        

Рис. 25

$F = a_0 (M+5m)$ .

Рассматривая уравнения двух брусков совместно, получим:

$3ma_0 = 2mg\ \text{или}\ a_0 = \frac 23 g.$

Тогда $F = \frac 23 g(M+5m)$ .

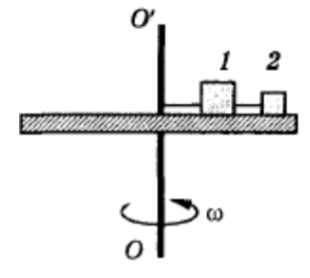
Пример 8. Горизонтальный диск вращают с угловой скоростью $\omega = 20\ \text{рад}/\text{с}$ вокруг вертикальной оси $OO'$ (рис. 25). На поверхности диска в гладкой радиальной канавке находятся грузы $1$ и $2$ массами $m_1 = 0,2\ \text{кг}$ и $m_2 = 0,1\ \text{кг}$ , радиусы их вращения $R_1 = 0,1\ \text{м}$ , $R_2 = 0,2\ \text{м}$ . Найти силы натяжения н и тей.

Решение. Рассмотрим силы, действующие на тела, и ускорения тел (рис. 26). Уравнение 2-го закона в проекциях имеет вид:         

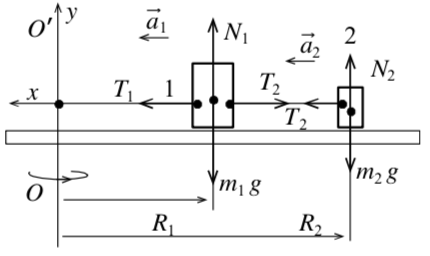Рис. 26

1) $T_1 - T_2 = m_1\omega^2R_1$ .

2) $T_2 = m_2\omega^2R_1$ .

$T_1 = T_2 + m_1\omega^2R_1 = \omega^2(m_1R_1 + m_2R_1).$

$T_1 = 16\ \text{Н}.$

$T_2 = 8\ \text{Н}$ .

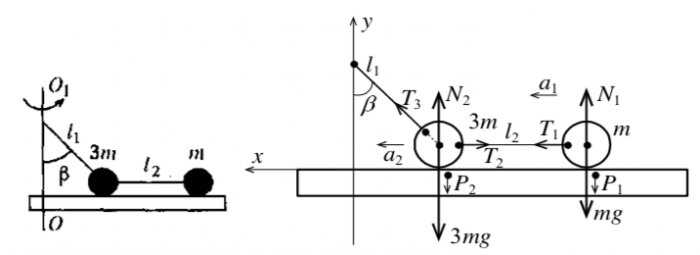
Рис. 27 Рис. 28

Пример 9. Два небольших по размерам груза с массами $3m$ и $m$ связаны нитью длиной $l_2$ и прикреплены к оси $OO_1$ нитью длиной $l_1$ , составляющей угол $\beta$ с осью $OO_1$ (см. рис. 27). Грузы находятся на горизонтальной платформе и вращаются вместе с ней вокруг вертикальной оси $OO_1$ . При какой постоянной угловой скорости грузы будут давить на платформу с одной и той же силой? Трение между грузами и платформой пренебрежимо мало.

Решение. На рисунке 28 изображены силы, действующие на грузы .

Для первого груза уравнения 2-го Закона Ньютона в проекции имеют вид:

$Ox:\quad T_1 = m\omega^2(l_2 + l_1\sin\beta)$ ;

$Oy:\quad N_1 = mg$ ,

$N_1 = P_1$ ;

Для второго груза:

$Ox:\quad T_3\sin\beta - T_2 = 3m\omega^2l_1\sin\beta$

$Oy:\quad T_3\cos\beta + N_2 = 3mg$

$N_2 = P_2$

$P_1 = P_2\ \text{(по условию)},$

$T_1 = T_2\ \text{(нить невесома)}.$

Из равенства $P_1 = P_2$ следует $N_1 = N_2$ , поэтому $T_3 = \frac{2mg}{\cos\beta}$ .

Тогда из проекции на $Ox$ следует:

$2mg\text{tg}\beta = m\omega^2(l_2+l_1\sin\beta + 3l_1\sin\beta)$

$\omega = \sqrt{\frac{2g\text{tg}\beta}{l_2 + 4l_1\sin\beta}}$ .         

Рис. 29

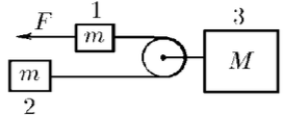
Пример 10. Найдите ускорения тел системы, изображённой на рисунке 29. Сила $F$ приложена по направлению нити к одному из тел массы $m$ . Участки нити по обе стороны от лёгкого блока, прикреплённого к телу массы $M$ параллельны.

Решение. Силы, действующие на тела, изображены на рисунке 30.

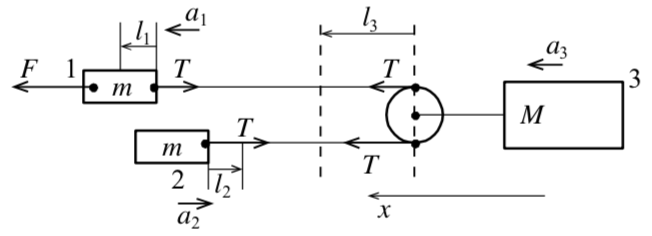
Рис. 30

Для первого тела:

$Ox: \quad F - T = m a_1$ .

Для второго тела:

$Ox:\quad -T = -ma_2$ .

Для третьего тела:

$Ox:\quad 2T = Ma_3$ .

Т. к. нить нерастяжима, то смещение второго тела к блоку $(l_2)$ равно смещению первого тела от блока $(l_1)$ . Т. к. блок сам смещается с ускорением, то к смещению первого блока добавится смещение $2l_3$ :

$a_1 = a_2 + 2a_3$ .

Из (2) и (3) следует $a_1 = a_3\frac{M}{2m}$ .

Тогда, решая совместно (1), (4) и (2), получим:

$a_3 = \frac{F}{M+2m}$ ,

тогда

$a_2 = \frac{F}{(M+2m)}\cdot\frac{M}{2m}\ и\ a_1 = \left(\frac{F}{M+2m}\right)\left(\frac{M+4m}{2m}\right)$ .

Комментарии