 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
Анализируя законы Кеплера, описывающие движение планет, И. Ньютон в 1667 году пришёл к открытию закона всемирного тяготения:
\[\boxed{F = G \frac{mM}{r^2}},\]
где гравитационная постоянная.
Все тела во Вселенной взаимно притягиваются друг к другу с силами прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними.
В такой форме закон справедлив только для двух тел, которые можно считать материальными точками. Однако можно доказать, что для двух однородных тел шарообразной формы эта форма записи закона тоже справедлива.
Измерить величину гравитационной постоянной удалось английскому физику Г. Кавендишу в 1798 году.
С помощью крутильных весов и свинцовых шаров ему удалось получить значение гравитационной постоянной:
\[\boxed{G = 6,67259 \cdot 10^{-11}\ \frac{\mathrm{Нм}^2}{\mathrm{кг}^2}}.\]
Второй закон Ньютона позволяет записать для силы, с которой тело притягивается к Земле: , тогда ускорение свободного падения на поверхности Земли (измерено Галилеем и Ньютоном), на расстоянии, большем радиуса на величину , ускорение свободного падения находится по формуле:
ускорение свободного падения на высоте от поверхности Земли.
Силой тяжести называют силу, с которой тело притягивается к планете:
\[\boxed{F = mg} - \mathrm{сила}\ \mathrm{тяжести}\]
Рассмотрим твёрдое тело, расположенное на горизонтальной неподвижной опоре: под действием силы тяжести тело деформируется. Если тело находится на опоре, то на нижний слой действуют все верхние слои, и, как следствие, этот слой деформируется наибольшим образом. На предпоследний слой действует меньшее количество слоёв, и он деформируется меньше. Таким образом, тело, бывшее прямоугольным, примет вид трапеции. Нижний слой приблизился при такой деформации к центру тела, а значит, возникла сила упругости, направленная в сторону, противоположную направлению смещения частиц при деформации. Сила упругости, возникшая внутри данного тела, направлена перпендикулярно опоре. Эту силу, созданную деформированным телом и приложенную к опоре, называют весом тела. Опора под действием веса деформируется. Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры (от слова normal - перпендикуляр).
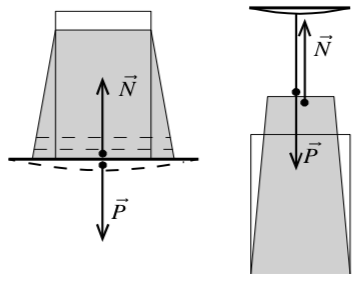 |
| Рис. 9 |
На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.
Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы – силы тяготения.
Невесомостью называют состояние тела, когда оно движется под действием только силы тяготения.
Так же легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.
Рассмотрим движение тела, помещённого в лифт. Пусть сам лифт движется с ускорением . Такое ускорение будет в двух случаях: 1) лифт поднимается равно ускорено, 2) лифт опускается равнозамедленно. Второй закон Ньютона для данного тела примет вид:
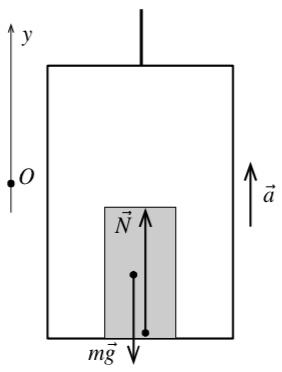 |
| Рис. 10 |
При рассмотрении данного движения из лабораторной неподвижной системы отсчёта увидим, что в проекции на вертикальную ось второй закон запишется следующим образом:
откуда
Но по третьему закону Ньютона знаем, что сила реакции опоры и вес тела равны и противоположны, следовательно:
тогда: вес тела, движущегося с ускорением, направленным вверх (рис. 10).
Не трудно проследить за тем, что мы получим, если ускорение тела будет направлено вниз.
В проекции на ось ускорение проецируется со знаком <<>>, что даст окончательную формулу для веса:
вес тела, движущегося с ускорением, направленным вниз.
Или в общем случае: вес тела, движущегося с ускорением.
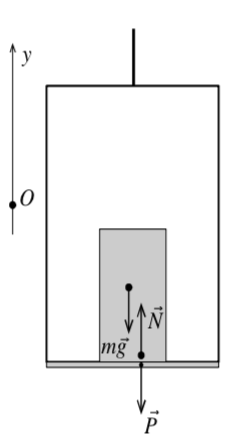 |
| Рис. 11а |
Подобным образом можно получить выражение для веса тела, движущегося равномерно по выпуклому участку дороги.
вес тела, движущегося с ускорением, направленным вниз (выпуклая дорога).
вес тела, движущегося с ускорением, направленным вверх (вогнутая дорога).
Важное дополнение:
Для рассматриваемой силы, называемой весом, важно понимать и уметь правильно изображать точку приложения этой силы.
На рисунке 11а показан лифт, у которого нет ускорения. Тогда сила тяжести равна силе реакции опоры . А по третьему закону Ньютона, сила реакции опоры равна весу тела. Точка приложения силы тяжести расположена в геометрическом центре тела, если тело однородно и правильной формы. Точка приложения силы реакции опоры должна быть изображена внутри тела вблизи с нижней поверхностью тела на линии действия силы тяжести. Последнее свойство на рисунке не выдержано для удобства изображения (иначе силы на рисунке будут накладываться друг на друга). Точка приложения веса тела находится внутри опоры (пола лифта) вблизи поверхности на линии действия силы реакции опоры.
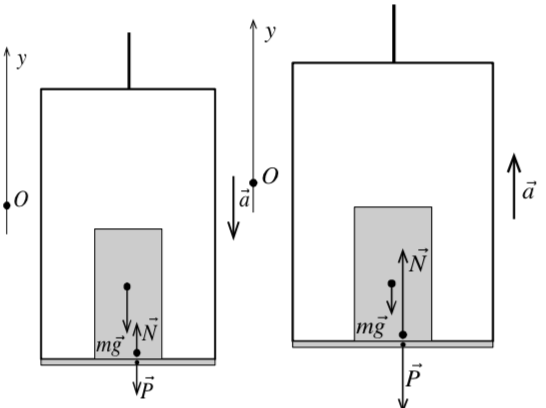 |
| Рис. 11б Рис. 11в |
На рисунке 11б ускорение лифта направлено вниз. Тогда сила реакции опоры меньше силы тяжести . А вес снова равен силе реакции опоры.
На рисунке 11в ускорение лифта направлено верх. Тогда сила реакции опоры больше силы тяжести . А вес снова равен силе реакции опоры.
Пример 5. Определить среднюю плотность Солнца, если его масса равна , а ускорение свободного падения на поверхности приблизительно составляет .
Решение. Так как , то можем найти радиус Солнца: . Считая Солнце шаром найденного радиуса и известной массы, можем найти среднюю плотность.
\[\rho = \frac MV = \frac{M}{\frac 43 \pi R^3} = \frac{3M}{4\pi \left(\frac{GM}{g}\right)^{\frac 32}} = \frac{3}{4\pi \sqrt M}\left(\frac gG\right)^{\frac 32}.\]
Количественно ответ будет таким: . Однако следует отметить, что этот ответ таков в данной модели. В действительности плотность Солнца не одинакова в недрах светила, и является функцией расстояния от центра. Мы же посчитали её везде одинаковой.
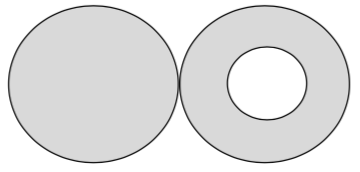 |
| Рис. 12 |
Пример 6. На сколько изменится сила притяжения двух одинаковых шаров, изготовленных из одинакового вещества плотностью , если у одного из них создать полость сферической формы, расположенную внутри одного из них в его центре? Изначально шары касались друг друга и притягивались с силой . Радиус полости равен половине радиуса шара (рис. 12).
Решение. Сила взаимодействия определяется законом всемирного тяготения. Т. к. формы тел шарообразные, то мы можем применить известную формулу закона: .
Массы тел равны, обозначим их , Масса извлечённой части . Новая сила будет меньше первоначальной на величину силы взаимодействия извлечённой части с первым шаром (принцип суперпозиции сил). Следовательно:
\[F_2 = G\frac{m_0 m}{(2R)^2} = G\frac{\frac 18 mm}{(2R)^2} = \frac 18 F\frac{mm}{(2R)^2} = \frac 18 F = 10\ \text{Н}.\]
Сила притяжения шаров станет меньше на , следовательно, станет равной .