 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
это вещества, не содержащие свободных зарядов.
В куске незаряженного диэлектрика, помещённого в электростатическое поле, появляются так называемые связанные заряды. В результате напряжённость поля внутри и вне диэлектрика изменяется по модулю и направлению по сравнению с тем, что было в соответствующих точках пространства до внесения диэлектрика. Природа возникновения связанных зарядов связана с явлением поляризации.
ориентация нейтральных молекул по полю из-за того, что молекулы были или стали под действием внешнего поля диполями.
Связанные заряды, возникшие в поляризованном диэлектрике, создают собственное электростатическое поле, которое накладывается на внешнее, противодействуя ему и пытаясь ослабить. Результирующее поле внутри диэлектрика становится отличным от внешнего.
Характеристикой однородного изотропного диэлектрика является диэлектрическая проницаемость $$ \varepsilon $$. Если граница такого диэлектрика перпендикулярна внешнему электрическому полю, то напряжённость поля в диэлектрике будет в $$ \varepsilon $$ раз меньше, чем в вакууме.
Напряжённость поля равномерно распределённого по сфере заряда, точечного заряда и бесконечной равномерно заряженной плоскости, помещённых в диэлектрик с диэлектрической проницаемостью $$ \varepsilon $$, будет в $$ \varepsilon $$ раз меньше, чем в вакууме. Для точечного заряда и сферы (при $$ r>R$$ ) вместо (2.2) и (2.3) справедливы формулы $$ E=k{\displaystyle \frac{\left|Q\right|}{\varepsilon {r}^{2}}}, {E}_{x}=k{\displaystyle \frac{Q}{\varepsilon {r}^{2}}}.$$
Для плоскости вместо (4.1) справедливо $$ E={\displaystyle \frac{\left|\sigma \right|}{2\varepsilon {\varepsilon }_{0}}}.$$
В бесконечном однородном и изотропном диэлектрике вместо формулы (2.1) закона Кулона можно записать
$$ F=k{\displaystyle \frac{\left|{q}_{1}\right|\left|{q}_{2}\right|}{\varepsilon {r}^{2}}}$$.
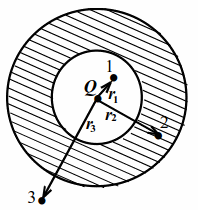 |
| Рис. 9.1 |
Точечный заряд $$ Q$$ находится в центре полого шара с диэлектрической проницаемостью $$ \varepsilon $$ (рис. 9.1). Найти напряжённость электрического поля в точках `1`, `2` и `3` на расстояниях $$ {r}_{1}$$, $$ {r}_{2}$$ и $$ {r}_{3}$$ от точечного заряда.
Пусть есть заряд $$ Q$$ в вакууме. С появлением слоя из диэлектрика напряжённость поля, перпендикулярная границам диэлектрика, изменяется только в диэлектрике, причём уменьшается в $$ \varepsilon $$ раз.
Поэтому
$$ {E}_{1}=k{\displaystyle \frac{\left|Q\right|}{{r}_{1}^{2}}}$$, $$ {E}_{2}=k{\displaystyle \frac{\left|Q\right|}{\varepsilon {r}_{2}^{2}}}$$, $$ {E}_{3}=k{\displaystyle \frac{\left|Q\right|}{{r}_{3}^{2}}}$$.