 ЗФТШ
ЗФТШ
- Обучение
- Поступление в ЗФТШ
- О ЗФТШ
- Учителям
- Лекторий
-
Курсы
- Заочное отделение
- Очное отделение
- Факультативы
9.1. Модель идеального газа в молекулярно-кинетической теории
Законы идеальных газов, найденные опытным путём, находят довольно простое объяснение в молекулярно-кинетической теории (МКТ). Она исходит при этом из упрощённых представлений о строении газа. Это обусловлено рядом причин, в частности, неточным знанием сил взаимодействия между молекулами. Однако, как оказывается, даже такая упрощённая модель газа позволяет найти уравнение состояния, правильно описывающее его поведение.
В молекулярно-кинетической теории принимается следующая идеализированная модель газа – идеальный газ. Молекулы газа считаются твёрдыми, абсолютно упругими шариками, причём размеры молекул малы по сравнению со средним расстоянием между ними. Это означает, что собственный суммарный объём молекул значительно меньше объёма сосуда, в котором находится газ. Взаимодействие между молекулами проявляется только при непосредственном столкновении их друг с другом. Между столкновениями молекулы движутся по инерции. Движение молекул подчиняется законам механики Ньютона.
Для нахождения уравнения состояния газа необходимо сделать ещё важное упрощающее предположение, а именно, считать движение любой молекулы газа беспорядочным, хаотичным.
Аккуратный вывод основного уравнения молекулярно-кинетической теории идеального газа требует принимать во внимание ряд моментов, например, наличие в газе молекул, движущихся с разными по величине скоростями, столкновения молекул между собой, характер столкновения отдельной молекулы со стенкой сосуда (упругий или неупругий). В разделе 7.3 будет рассмотрен упрощённый вариант вывода основного уравнения молекулярно-кинетической теории.
9.2. Давление идеального газа
Давление, которое оказывает газ на стенку сосуда, есть результат ударов молекул газа о стенку. Если бы в сосуде содержалось всего несколько молекул, то их удары следовали бы друг за другом редко и беспорядочно. Поэтому нельзя было бы говорить ни о какой регулярной силе давления, действующей на стенку. Стенка подвергалась бы отдельным практически мгновенным бесконечно малым толчкам. Если же число молекул в сосуде очень велико, то велико и число ударов их о стенку сосуда. Одновременно о стенку сосуда ударяется громадное количество молекул. Очень слабые силы отдельных ударов складываются при этом в значительную по величине и почти постоянную силу, действующую на стенку. Среднее по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа, с которым имеет дело термодинамика.
Пусть в сосуде объёма $$ V$$ находятся $$ N$$ одинаковых молекул идеального газа, а $$ {m}_{0}$$ – масса одной молекулы. В рамках молекулярно-кинетической теории показывается, что давление $$ p$$ газа определяется выражением:
, (11)
где $$ n=N/V$$ – концентрация молекул газа, – среднее значение квадрата скорости молекулы. Выражение (11) называют основным уравнением молекулярно-кинетической теории идеального газа.
Заметим, что величина есть средняя кинетическая энергия поступательного движения молекулы. Поэтому полученную формулу можно представить в другом виде:
. (12)
Ниже приводится один из способов вывода уравнения (11). Данный раздел при первом прочтении можно пропустить.
9.3* Вывод основного уравнения МКТ идеального газа
Вычислим среднее давление газа на стенку сосуда.
Для простоты будем считать, что удар молекулы о стенку происходит абсолютно упруго, а сама стенка идеально гладкая и молекула после удара отражается от неё под тем же углом, под каким она падала на стенку (см. рис. 11), или, как говорят, зеркально (однако ясно, что никаких гладких стенок не существует: ведь сама стенка состоит из молекул).
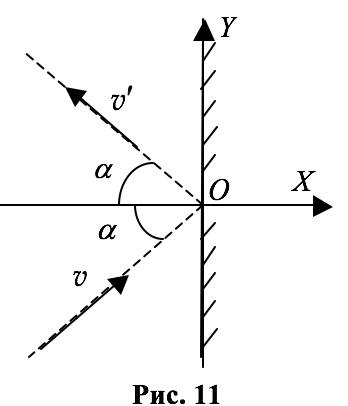 |
Введём систему координат, направив ось $$ OX$$ перпендикулярно стенке, а ось $$ OY$$ – вдоль стенки (см. рис. 11).
Пронумеруем все молекулы от $$ i=1$$ до $$ i=N$$. Пусть $$ {v}_{i,x},({v}_{i,x}>0) -$$ проекция скорости $$ i$$-ой молекулы на ось $$ OX$$ до удара. При абсолютно упругом ударе о стенку проекция скорости на ось $$ OX$$ изменяет знак: $$ {v}_{i,x}^{\text{'}}=-{v}_{i,x}$$. Изменение проекции импульса молекулы на ось $$ OX$$ при столкновении молекулы со стенкой равно:
$$ \mathrm{\Delta }{p}_{i,x}={m}_{0}{v}_{i,x}^{\text{'}}-{m}_{0}{v}_{i,x}=-2{m}_{0}{v}_{i,x}$$,
а передаваемый стенке импульс равен:
$$ \mathrm{\Delta }{p}_{i,x,\mathrm{стен}}=-\mathrm{\Delta }{p}_{i,x}=2{m}_{0}{v}_{i,x}$$.
Так как давление газа не зависит от формы сосуда, возьмём для простоты сосуд в форме куба с ребром $$ l$$. Тогда промежуток времени между двумя последовательными столкновениями молекулы с одной и той же стенкой составит $$ {\tau }_{i}=2l/{v}_{i,x}$$, а за большой интервал времени $$ t$$ она столкнётся со стенкой $$ {N}_{\mathrm{столк},i}=t/{\tau }_{i}$$ раз. Переданный стенке одной молекулой за это время импульс равен:
`2m_0v_(i,x)*N_("столк",i)=2m_0v_(i,x)*(v_(i,x)t)/(2l)=m_0v_(i,x)^2*t/l`.
Так как в сосуде находятся $$ N$$ молекул, то полный переданный стенке импульс всех молекул равен:
$$ \mathrm{\Delta }{p}_{x,\sum }=\sum _{i=1}^{i=N}\Delta {p}_{i,x,\mathrm{стен}}={\displaystyle \frac{{m}_{0}t}{l}}\sum _{i=1}^{i=N}{v}_{i,x}^{2}$$.
Среднюю силу давления на стенку можно получить, разделив полный передаваемый стенке импульс на время $$ t$$:
`F_(x,"ср")=(Deltap_(x,sum))/t=m_0/l sum_(i=1)^(i=N) v_(i,x)^2`,
а давление $$ p -$$ разделив эту силу на площадь стенки $$ S={l}^{2}$$:
`p=(F_(x,"ср"))/S=m_0/l^3 sum_(i=1)^(i=N) v_(i,x)^2=m_0/V sum_(i=1)^(i=N) v_(i,x)^2`.
Здесь учтено, что объём сосуда $$ V={l}^{3}$$. Если ввести среднее значение квадрата проекции скорости одной молекулы:
`bar(v_x^2)=1/N sum_(i=1)^(i=N) v_(i,x)^2`,
то для давления $$ p$$ получаем:
$$ p={\displaystyle \frac{{m}_{0}N}{V}}\overline{{v}_{x}^{2}}$$.
Входящую в это выражение величину $$ \overline{{v}_{x}^{2}}$$ можно выразить через среднее значение квадрата скорости молекулы. Из соотношения $$ {v}^{2}={v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}$$ для средних значений имеем: $$ \overline{{v}^{2}}=\overline{{v}_{x}^{2}}+\overline{{v}_{y}^{2}}+\overline{{v}_{z}^{2}}$$. Так как движение молекул беспорядочное, то все направления движения равновероятны и средние значения квадратов проекций на любое направление должны быть равны $$ \overline{{v}_{x}^{2}}=\overline{{v}_{y}^{2}}=\overline{{v}_{z}^{2}}$$. Отсюда получаем: $$ \overline{{v}^{2}}=3\overline{{v}_{x}^{2}}$$, что позволяет записать выражение для давления в виде:
$$ p={\displaystyle \frac{1}{3}}{\displaystyle \frac{{m}_{0}N}{V}}\overline{{v}^{2}}, \mathrm{или} p={\displaystyle \frac{1}{3}}{m}_{0}n\overline{{v}^{2}}$$,
где $$ n=N/V$$ концентрация молекул газа.