Статьи

• 
  2.1 Среда программирования. Ввод / вывод информации

  • 17 января 2023 г.
  • 0 комментариев
  • 309 просмотров

  У языка программирования Pascal есть свой алфавит. В него входят: латинские буквы (26), цифры от 0 до 9, специальные знаки (+,-, круглые, квадратные и фигурные скобки, точка, запятая, точка с запятой, <, >, <=, >=, $ и др.), а также служебные слова (из английского языка: begin, end, for, while и др.). 

  При написании программы для переменных величин вводятся обозначения. Такое обозначение в языке программирования называют именем величины. Имя величины в Паскале – это слово из букв, цифр и знаков подчеркивания, начинающегося с буквы. Каждое имя соответствует некоторой ячейке памяти, куда записывается значение переменной величины. 

  Поскольку в ячейку можно записать одно за другим сколько угодно данных, имя также называют переменной или именем переменной. Ячейка - понятие условное, это последовательность разного количества байтов для разных данных. Любой символ клавиатуры занимает один байт. Поэтому для каждой переменной надо указать ее тип, чтобы транслятор (программа, переводящая на язык машинных команд) знал, сколько места в памяти она будет занимать.

  Числа в Паскале. Числа в Паскале различаются как целые и действительные (вещественные). Целое число по внешнему виду такое же, как обычно: знак «+» можно не указывать. Вещественные числа, несмотря на одинаковое представление в памяти компьютера, могут иметь вид с фиксированной и с плавающей точкой.

  Числа с фиксированной точкой. Числа с фиксированной точкой похожи на десятичные, только целая часть от дробной отделяется не запятой, а точкой: -7.23, 897.5, -0.11. При выполнении действий с фиксированной точкой может получиться результат, целая часть которого содержит больше разрядов, чем объем ячейки памяти. 

  Числа с плавающей точкой. Чтобы избежать переполнения ячейки памяти, используют представление вещественных чисел с плавающей точкой. В этом случае число представляется в виде мантиссы и порядка. Мантисса – это последовательность цифр, изображающих число, а порядок определяет положение точки в этой последовательности.

  Для работы с числами используют шесть операций: 

  1. « + » - сложение, 
  2. « - » - вычитание, 
  3. « / » - деление, 
  4. « * » - умножение, 
  5. mod – нахождение остатка от деления,
  6. div – деление нацело.

  Что такое арифметическое выражение, из чего оно может состоять? Из имен, чисел, знаков арифметических действий и математических функций конструируются арифметические выражения. Для указания порядка действий используются только круглые скобки, их может быть несколько, главное, чтобы количество открывающих скобок равнялось количеству закрывающих.

  Математические функции. В Паскале во многом совпадают с общепринятыми: sin(x), cos(x), ln(x). Для возведения аргумента в квадрат используется обозначение sqr(x), для извлечения квадратного корня sqrt(x), а модуль обозначается abs(x). В качестве аргумента каждой функции может быть арифметическое выражение.

  Алгоритм преобразования данных на Паскале состоит из операторов – укрупненных команд. Каждый оператор преобразуется транслятором в последовательность машинных команд. Основное преобразование данных, выполняемых компьютером, - присваивание переменной нового значения. 

  Общий вид оператора присваивания

  Имя переменной: = арифметическое выражение;

  Знак «: =» читается «присвоить». Точка с запятой в конце записи оператора является обязательной.

  Как работает оператор присваивания? При выполнении оператора присваивания рассматривается арифметическое выражение, из ячеек оперативной памяти, соответствующих стоящим там именам, вносятся в процессор значения и выполняются указанные действия над данными. Полученный результат записывается в ячейку памяти, имя которой указано слева от знака присваивания.

  Рассмотрим пример использования оператора присваивания 

  1. x: =5; {переменной x присвоить значение 5} 
  2. a: = b+c; {из ячеек b и c считываются заранее помещенные туда данные, вычисляется сумма, результат записывается в ячейку a} 
  3. i: =i+1; {значение переменной увеличивается на 1}
• 
  Блок-схемы и алгоритмы

  • 30 августа 2022 г.
  • 0 комментариев
  • 250 просмотров

  Здесь будет текст

• 
  Блок-схемы и алгоритмы

  • 29 августа 2022 г.
  • 0 комментариев
  • 2824 просмотра

  В рамках этого задания мы займёмся развитием алгоритмического мышления, и будем рассматривать различные положения теории алгоритмов. Прежде всего, определим понятие «Алгоритм».
  
  

  ОПРЕДЕЛЕНИЕ

  Алгоритм – это последовательность действий, преобразующая исходные данные в результат и обладающая некоторыми свойствами.
  
  

  Приведённое определение не является строгим, поскольку в нём присутствует ссылка на «некоторые свойства». Чтобы подробно описать понятие Алгоритма рассмотрим эти свойства.

   

  свойства

  1) Конечность. Последовательность действий является алгоритмом только тогда, когда  преобразование любых допустимых входных данных в результат происходит за конечное число шагов.

  Например, можно составить алгоритм для решения задачи: «Выпишите в строчку все цифры двадцатеричной системы счисления», но нельзя составить алгоритм для решения задачи: «Выпишите все натуральные числа», поскольку в этом случае количество действий – бесконечное.

  2) Детерминированность. Это свойство обозначает, что если применить алгоритм сколь угодно раз к одним и тем же входным данным, результат всегда получится одинаковым.

  3) Дискретность. О данном понятии рассказывалось в рамках предыдущего задания по алгебре логики. Свойство дискретности применительно к алгоритму обозначает, что выполнение алгоритма разбивается на последовательность законченных действий. То есть каждое действие должно завершиться, прежде чем начнётся следующее.

  4) Понятность. Чтобы описать это свойство, стоит упомянуть, что алгоритм всегда рассчитан на некоторого конкретного исполнителя, который умеет производить некоторый набор действий. Свойство понятности заключается в том, что все действия, входящие в алгоритм должны принадлежать к набору действий исполнителя. Набор действий, которые может исполнить исполнитель, называется «системой команд». Стоит отметить, что исполнитель не должен ничего додумывать. Его задача – исключительно исполнять команды.

  5) Массовость. Это свойство означает, что алгоритм пишется не для одних конкретных входных данных, а для некоторого множества задач. В отличие от предыдущих свойств, которые являются просто неотъемлемой частью любого алгоритма, свойство массовости является ещё и характеристикой алгоритма, то есть можно говорить, что алгоритм `"A"` является более массовым, чем алгоритм `"C"`. Это будет означать, что все задачи, которые можно решить алгоритмом C также можно решить и алгоритмом `"A"`, но существуют задачи, которые можно решить алгоритмом `"A"` и нельзя решить алгоритмом `"C"`.

  
  
  Рассмотрим несколько примеров исполнителей алгоритмов.
  
  

  ПРИМЕРЫ  ИСПОЛНИТЕЛЕЙ АЛГОРИТМОВ

  1) Исполнителем является любой человек сознательного возраста. Здесь могут решаться такие задачи как переход улицы, приём пищи, приготовление сладкого стола, украшение комнаты и т. д. Для всех перечисленных задач можно составить алгоритмы. Например, классический алгоритм перехода улицы формулируется так: «Посмотри налево, если ближе некоторого расстояния нет машин, иди до середины дороги, остановись, посмотри направо, и если ближе некоторого расстояния нет машин, то иди до конца». В приведённой формулировке есть переменная величина – безопасное расстояние, на котором могут находиться машины. Она зависит от конкретного человека, поэтому для конкретного человека наш алгоритм надо будет уточнять.

  2) Исполнителем является человек, обладающий определёнными умениями. Один из простых примеров задач для такого исполнителя – это удаление аппендицита. Алгоритм составить можно, но исполнять его может не любой человек, а только тот, кто обладает умением хирургического вмешательства.

  3) Исполнителем может быть робот, живущий в прямоугольном лабиринте и умеющий ходить в разные стороны. В этом случае можно поставить задачу перехода из одной точки лабиринта в другую и составить алгоритм её решения.

  4) Исполнителем может являться компьютер. Здесь, как и для человека, можно поставить огромный набор задач. Примеры рассмотрим в дальнейшем.

  Как уже упоминалось выше, у каждого исполнителя есть своя система команд – набор простых действий, которые может выполнить данный исполнитель. Если мы составляем алгоритм для этого исполнителя, то все шаги алгоритма должны входить в систему команд исполнителя. Наиболее простым из рассмотренных исполнителей является робот в лабиринте. Его система команд достаточно простая, и мы можем легко выписать её:

         «ИДИ ВПРАВО НА 1 КЛЕТКУ»

         «ИДИ ВЛЕВО НА 1 КЛЕТКУ»

         «ИДИ ВВЕРХ НА 1 КЛЕТКУ»

         «ИДИ ВНИЗ НА 1 КЛЕТКУ»

         «ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СПРАВА»

         «ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СЛЕВА»

         «ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СВЕРХУ»

         «ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СНИЗУ»

  Очевидно, что уже у такого простого исполнителя набор команд неоднородный. Есть команды, результатом которых является сдвиг робота, а есть команды проверки, результатом которых является логическое значение  «Истина» или «Ложь». (Подробно о логических значениях рассказывалось в рамках прошлого задания). Наличие команд проверки позволит нам ввести алгоритмические конструкции ветвления и цикла, но об этом чуть позже.
  
  При изучении алгоритмов для лучшего понимания иногда мы будем пользоваться псевдоисполнителем алгоритмов, языком которого является блок-схема. Блок-схема является достаточно удобным представлением алгоритма, чтобы проследить логику его выполнения. Состоит она из блоков и связей между блоками. Связи обозначаются стрелками, которые показывают последовательность исполнения блоков. Из блоков нас будут интересовать 4 типа:
  
  

  ТИП БЛОКА
  
  

  1) Начало/Конец алгоритма 

  

  2) Получение исходных данных/Выдача результатов

   

  3) Линейное вычисление

  

  4) Ветвление 

  
  
  

  В блок-схемы линейный участок обозначается прямоугольником. Все команды, записанные в прямоугольнике, исполняются ровно в том порядке, в котором они записаны (будем считать, что сверху вниз). Аналогично Паскалю, будем отделять команды друг от друга в линейном блоке точкой с запятой. Присваивание также будем обозначать символом «`:=`», а вот арифметическое выражение можно записывать, используя как синтаксис Паскаля, так и математики (этим можно пользоваться при решении задач). Аналогично с арифметическим, логическое выражение можно записывать, используя как синтаксис Паскаля, так и алгебры логики.

  Алгоритм на языке блок-схемы всегда начинается с блока начала, затем идёт блок ввода входных данных, если они есть, далее блок вычислений, затем блок вывода результата и блок завершения алгоритма. В качестве примера рассмотрим блок-схему вычисления площади треугольника по длинам его `3` сторон с использованием формулы Герона. Входными данными в этой задаче являются длины сторон, а результатом – значение площади. Соответственно, мы будем решать задачу, используя пять переменных. Три стороны – a, b, c. Площадь – s.  И полупериметр – p. Будем считать, что стороны всегда будут заданы таким образом, что треугольник существует. Рассмотрим блок-схему решения этой задачи:

  
  

  В блок-схемы линейный участок обозначается прямоугольником. Все команды, записанные в прямоугольнике, исполняются ровно в том порядке, в котором они записаны (будем считать, что сверху вниз). Аналогично Паскалю, будем отделять команды друг от друга в линейном блоке точкой с запятой. Присваивание также будем обозначать символом «`:=`», а вот арифметическое выражение можно записывать, используя как синтаксис Паскаля, так и математики (этим можно пользоваться при решении задач). Аналогично с арифметическим, логическое выражение можно записывать, используя как синтаксис Паскаля, так и алгебры логики.

  Алгоритм на языке блок-схемы всегда начинается с блока начала, затем идёт блок ввода входных данных, если они есть, далее блок вычислений, затем блок вывода результата и блок завершения алгоритма. В качестве примера рассмотрим блок-схему вычисления площади треугольника по длинам его `3` сторон с использованием формулы Герона. Входными данными в этой задаче являются длины сторон, а результатом – значение площади. Соответственно, мы будем решать задачу, используя пять переменных. Три стороны – a, b, c. Площадь – s.  И полупериметр – p. Будем считать, что стороны всегда будут заданы таким образом, что треугольник существует. Рассмотрим блок-схему решения этой задачи:

  
  

  
  

• 
  Тест

  • 29 августа 2022 г.
  • 0 комментариев
  • 467 просмотров

  Тест

• 
  Примеры решения задач

  • 17 ноября 2017 г.
  • 0 комментариев
  • 80409 просмотров

  Пример 1. Какие силы действуют на человека во время ходьбы? Какая сила приводит его в движение?

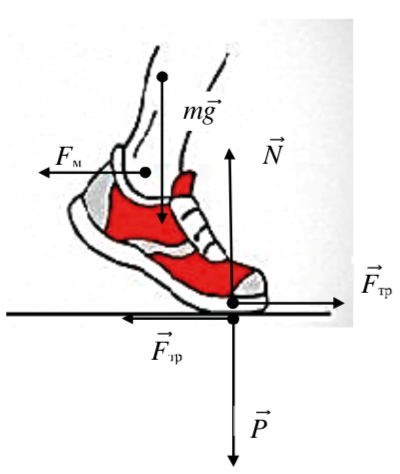  Рис. 15

  Решение: На человека всегда действует сила тяжести $(m\vec g)$. Она приложена ко всем частям организма, но принято её изображать приложенной к центру масс (на рис. 15 это не так). Во время ходьбы человек мышечными усилиями толкает ногу назад, относительно центра масс (туловища). На рисунке эта сила обозначна как $\vec F_\mathrm{м}$. Нога бы начала такое движение, если бы не было сцепления протектора подошвы и поверхности асфальта (пола). Вдоль поверхности возникает сила трения покоя. Нога толкает этой силой асфальт влево $(\vec F_\mathrm{тр})$, а асфальт толкает ногу вправо $(\vec F_\mathrm{тр})$, приводя её в движение относительно асфальта. Человек оказывает на поверхность асфальта действие, называемое весом $(\vec P)$, а на человека действует противоположная сила реакции опоры $(\vec N)$.

  Пример 2. С каким ускорением будет двигаться тело массой $3\ \text{кг}$ по поверхности стола с коэффициентом трения $0,3$, если к нему приложить силу $10\ \text{Н}$ под углом $30^\circ$ к горизонту?










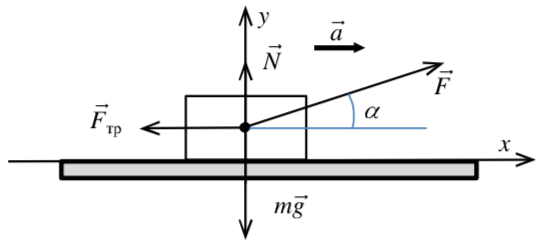  Рис. 16

  Решение. Расставим силы. При расстановке сил пользуются, преимущественно, двумя моделями: 1) все силы прикладывают к центру масс тела, который символизирует материальную точку, в качестве которой рассматривается тело; 2) точки приложения сил изображают там, где сила приложена. Во втором случае требуется применять ряд дополнительных правил, которые на первых порах излишне усложняют решение. На данном рисунке 16 применены правила первой модели.

  Далее запишем 2-ой закон Ньютона в векторной форме:

  $m\vec g + \vec F_\mathrm{тр} + \vec N + \vec F = m\vec a$.

  Теперь пишем проекции этого уравнения на оси $Ox$ и $Oy$. Отметим, что оси удобнее всего выбирать из принципа удобства, что чаще всего соответствует направлению одной из осей вдоль ускорения, а второй оси перпендикулярно первой. Еcли движутся несколько тел, то для каждого тела можно выбирать свою удобную пару осей.

  $Ox:\quad -F_\mathrm{тр} + F\cos \alpha = ma,$

  $Oy:\quad -mg + N + F\sin \alpha = 0.$

  Вспомогательное уравнение (формула Кулона – Амонтона):

  $$F_\text{тр} =\mu \cdot N$$

  Решая скалярную тройку уравнений, получим:

  $a = \frac Fm (\mu\cdot \sin \alpha + \cos\alpha) - \mu g$.

  Подставим числовые значения и получим: $a\approx 0,39\ \frac{\text{м}}{\text{с}^2}$.

  При достаточной тренировке в решении задач запись в векторном виде становится излишней, и пишем сразу проекции на оси. На начальном этапе обучения пропускать эту запись не следует.










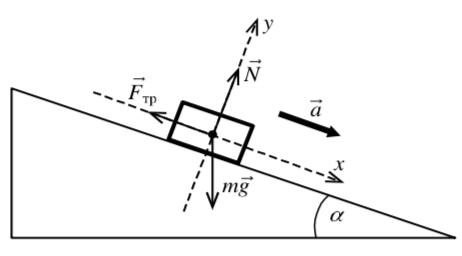  Рис. 17

  Пример 3. По наклонной плоскости с углом наклона при основании $\alpha = 30^\circ$ соскальзывает тело. Найти ускорение тела при коэффициенте трения поверхности и тела, равным $0,2$.

  Решение. На рисунке 17 расставим силы и выберем оси координат из принципа удобства (одна из осей вдоль ускорения).

  Запишем уравнение второго закона Ньютона в векторном виде:

  $m\vec g + \vec F_\mathrm{тр} + \vec N = m\vec a$.

  Далее проецируем его на оси координат:

  $Ox:\quad -F_\mathrm{тр} + mg\cdot \sin \alpha = ma$,

  $Oy:\quad -mg\cdot\cos\alpha + N = 0$

  Добавим формулу Кулона-Амонтона:

  $F_\mathrm{тр} = \mu\cdot N$.

  Решая систему уравнений, получим:

  $a = g(\sin\alpha-\mu\cos\alpha)$.

  Числовой ответ даёт значение: $a\approx 3,27\ \frac{\text{м}}{\text{с}^2}$.

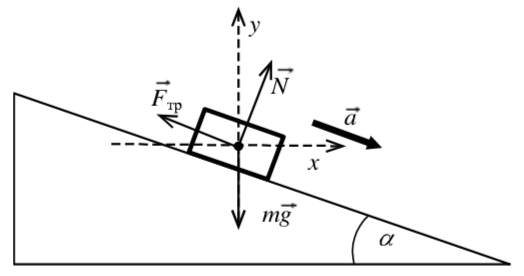
  Рассмотрим способ с другими направлениями осей (рис. 18) (неудобными)

  

  $Ox:\quad -F_\mathrm{тр}\cdot\cos\alpha + N\cdot\sin\alpha = ma\cdot\cos\alpha,$

  $Oy:\quad -mg+N\cdot\cos\alpha = -a\cdot\sin\alpha$.

  Добавим формулу Кулона-Амонтона: $F_\mathrm{тр} = \mu\cdot N$.

  Решение этой системы уравнений так же приведёт к тому же ответу (проверьте самостоятельно), но путь достижения цели будет и длиннее, и сложнее.

  Пример показывает рациональность предлагаемого принципа удобства.










  Рис. 19

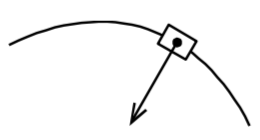
  Пример 4. Коэффициент трения между резиной и асфальтом $0,7$. Какой должна быть ширина дороги, чтобы на ней смог развернуться мотоциклист без уменьшения скорости, если его скорость равна $54\ \text{км}/\text{ч}$?

  Если мотоциклист планирует развернуться, не уменьшая скорости, то движение его будет равномерным по окружности. Сила, приводящая к изменению направления скорости, будет сообщать центростремительное (нормальное) ускорение (рис. 19) . Этой силой будет сила трения.

  Решение. Выберем ось $Ox$ вдоль ускорения (рис. 20) . Запишем 2-й закон Ньютона в проекции на эту ось:










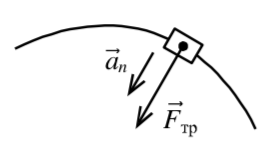  Рис. 20

  $F_\mathrm{тр} =ma_n = m\frac{v^2}{R}$.

  Так как $F_\mathrm{тр} = \mu N$, а $N = mg$, то $\mu mg = m\frac{v^2}{R}$, откуда $R = \frac{v^2}{\mu g}$, тогда для разворота нужна ширина:

  $l = 2R;\quad l = \frac{2v^2}{\mu g};\quad l = 64,3\ \text{м}$

  Из ответа видим, что для разворота на реальной дороге необходимо сниизить скорость.

  Пример 5. Два тела массами $m_1 = 2\ \text{кг}, \ m_2 = 3\ \text{кг}$ связаны нитью. Первое тело тянут вправо с силой $F = 15\ \text{Н}$ по поверхности с коэффициентом трения $\mu = 0,1$. Определите силу натяжения нити, связывающей тела. С каким ускорением движутся тела? Оборвётся ли нить, если поместить тела на поверхность с коэффициентом трения $0,3$, а максимальная сила натяжения нити  $10\ \text{Н}$?

  Решение. Расставим силы, действующие на тела (рис. 21):

  

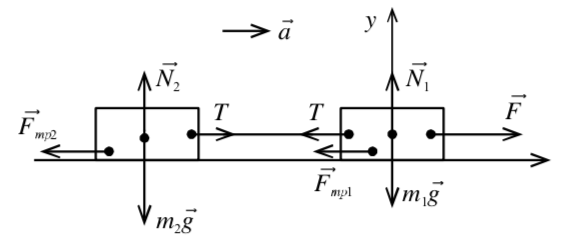
  Рис. 21

  Выберем ось $Ox$ вдоль силы $\vec F$ и ось $Oy$ перпендикулярно ей.

  Второй закон Ньютона для двух тел в проекции на ось $Ox$:

  $F - F_\mathrm{тр1} - T + T - F_\mathrm{тр2} = (m_1 + m_2)a$,

  для первого тела на ось $Oy$:

  $N_1 - m_1g = 0,\ \mathrm{тогда}\ F_\mathrm{тр1} = \mu m_1 g$;

  для второго тела:

  $N_2 - m_2g = 0 \Rightarrow \ F_\mathrm{тр2} = \mu m_2g$.

  Выразим ускорение из проекции $Ox$, подставляя силы трения:

  $a = \frac{F}{m_1 + m_2}-\mu g$,

  $a = 2\ \frac{\text{м}}{\text{с}^2}$.

  Теперь запишем второй закон Ньютона для второго тела:

  $Ox:\quad T-F_\mathrm{тр2} = m_2 a$,

  откуда 

  $T = F_\mathrm{тр2} + m_2 a$,

  $T = m_2(\mu g + a)$,

  $T = \frac{m_2}{m_1 + m_2}F = 9\ \text{Н}$.

  Если $\mu = 0,3$, то $a = 0$, тела движутся равномерно, а сила натяжения нити останется прежней, $T = 9\ \text{Н} < 10\ \text{Н}$. Нить не порвётся.

  Пример 6. На вершине наклонной плоскости, с углом при основании $30^\circ$ укреплён неподвижный блок. Через блок перекинута невесомая и нерастяжимая нить . К нити привязаны два тела: $m_1 = 3\ \text{кг}$ со стороны плоскости и $m_2 = 4\ \text{кг}$ с другой. Коэффициент трения при движении тела по поверхности равен $0,2$. Какова сила натяжения нити и ускорения тел?

  Решение. Силы, действующие на тела, представлены на рисунке 22.

  

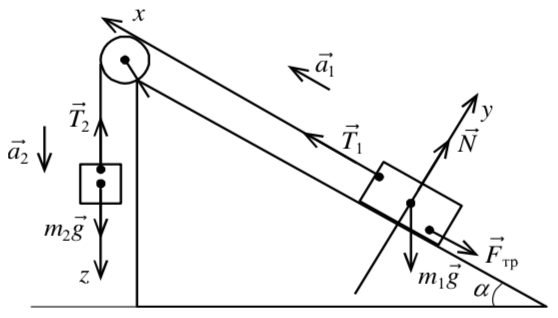
   Рис. 22

  Запишем 2-ой закон Ньютона для первого тела в проекциях:

  $Ox:\quad T_1 - F_\mathrm{тр} - m_1 g\sin \alpha = m_1 a_1$,

  $O_y:\quad N-m_1g\cos\alpha = 0$.

  С учётом, что $F_\mathrm{тр} = \mu N$, получим $T_1 - \mu m_1 g\cos\alpha - m_1g\sin\alpha = m_1 a_1$.

  Для второго тела в проекции на $Oz$:

  $m_2g - T_2 = m_2a_2$.

  Решая совместно два уравнения, получим (учитывая, что $a_1 = a_2 = a$ и $T_1 = T_2 = T$)

  $a = \frac{m_2 - m_1\sin\alpha - \mu m_1\cos\alpha}{m_1 + m_2}g$,

  $a \approx 2,83\ \text{м}/\text{с}^2$.










  Рис. 23

  Из этих же уравнения получим силу натяжения нити:

  $T = g\frac{m_1m_2}{m_1 + m_2}(1 + \sin\alpha + \mu\cos\alpha)$

  $T \approx 28,7\ \text{Н}$.

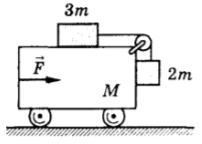
  Пример 7. Какую горизонтальную силу $F$ нужно приложить к тележке массой $M$, чтобы бруски массой $2m$ и $3m$ (рис. 23) относительно неё не двигались? Трением пренебречь.

  Решение. На рисунке 24 изображены силы, действующие на тела.

  

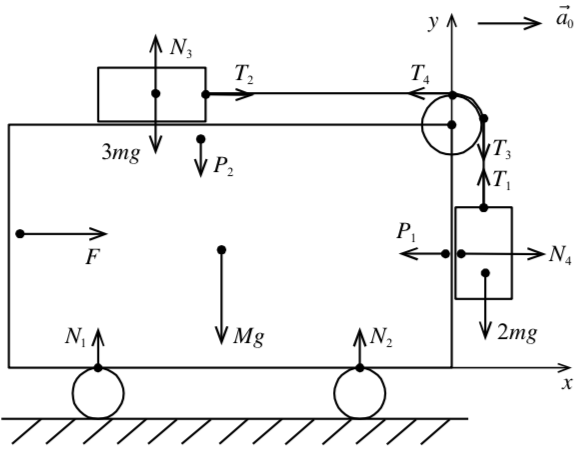
  Рис. 24

  Если трения нет и бруски неподвижны относительно тележки, то 2-й закон Ньютона в проекциях для тел примет вид:

  1) для тележки:

  $Ox:\quad F - P_1 - T_4 = Ma_0$,

  $Oy:\quad N_1 + N_2 - Mg - P_2 - T_3 = 0$;

  2) для бруска $3m$:

  $Ox:\quad T_2 = 3ma_2$,

  $Oy:\quad N_3 - 3mg = 0,\quad N_3 = P_2$;

  3) для бруска $2m$:

  $Ox:\quad N_4 = 2ma_1$,

  $Oy:\quad T_1-2mg = 0, \quad N_4 = P_1$;

  4) $T_1 = T_2 = T_3 = T_4\quad \text{(нить невесома)},$

  5) $a_1 = a_2 = a_0\quad \mathrm{(нить}\ \mathrm{нерастяжима)}$ 

  Решая совместно получим:









  Рис. 25

  $F = a_0 (M+5m)$.

  Рассматривая уравнения двух брусков совместно, получим:

  $3ma_0 = 2mg\ \text{или}\ a_0 = \frac 23 g.$

  Тогда $F = \frac 23 g(M+5m)$.

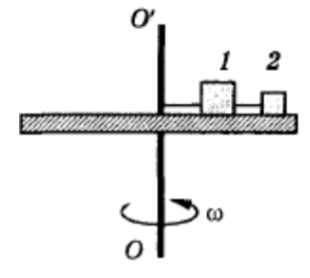
  Пример 8. Горизонтальный диск вращают с угловой скоростью $\omega = 20\ \text{рад}/\text{с}$ вокруг вертикальной оси $OO'$ (рис. 25). На поверхности диска в гладкой радиальной канавке находятся грузы $1$ и $2$ массами $m_1 = 0,2\ \text{кг}$ и $m_2 = 0,1\ \text{кг}$, радиусы их вращения $R_1 = 0,1\ \text{м}$, $R_2 = 0,2\ \text{м}$. Найти силы натяжения н и тей.

  Решение. Рассмотрим силы, действующие на тела, и ускорения тел (рис. 26). Уравнение 2-го закона в проекциях имеет вид:










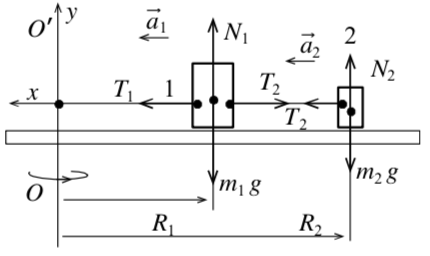  Рис. 26

  1) $T_1 - T_2 = m_1\omega^2R_1$.

  2) $T_2 = m_2\omega^2R_1$.

  $T_1 = T_2 + m_1\omega^2R_1 = \omega^2(m_1R_1 + m_2R_1).$

  $T_1 = 16\ \text{Н}.$

  $T_2 = 8\ \text{Н}$.

  

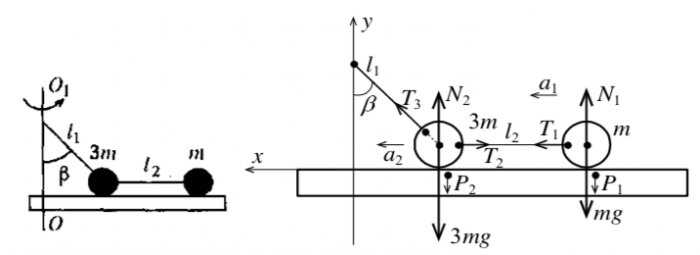
  Рис. 27                                                                                                           Рис. 28

  Пример 9. Два небольших по размерам груза с массами $3m$ и $m$ связаны нитью длиной $l_2$ и прикреплены к оси $OO_1$ нитью длиной $l_1$, составляющей угол $\beta$ с осью $OO_1$ (см. рис. 27). Грузы находятся на горизонтальной платформе и вращаются вместе с ней вокруг вертикальной оси $OO_1$. При какой постоянной угловой скорости грузы будут давить на платформу с одной и той же силой? Трение между грузами и платформой пренебрежимо мало.

  Решение. На рисунке 28 изображены силы, действующие на грузы .

  Для первого груза уравнения 2-го Закона Ньютона в проекции имеют вид:

  $Ox:\quad T_1 = m\omega^2(l_2 + l_1\sin\beta)$;

  $Oy:\quad N_1 = mg$,

  $N_1 = P_1$;

  Для второго груза:

  $Ox:\quad T_3\sin\beta - T_2 = 3m\omega^2l_1\sin\beta$

  $Oy:\quad T_3\cos\beta + N_2 = 3mg$

  $N_2 = P_2$

  $P_1 = P_2\ \text{(по условию)},$

  $T_1 = T_2\ \text{(нить невесома)}.$

  Из равенства $P_1 = P_2$ следует $N_1 = N_2$, поэтому $T_3 = \frac{2mg}{\cos\beta}$.

  Тогда из проекции на $Ox$ следует:

  $2mg\text{tg}\beta = m\omega^2(l_2+l_1\sin\beta + 3l_1\sin\beta)$

  $\omega = \sqrt{\frac{2g\text{tg}\beta}{l_2 + 4l_1\sin\beta}}$.










  Рис. 29

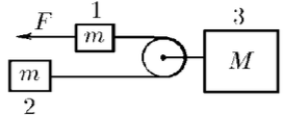
  Пример 10. Найдите ускорения тел системы, изображённой на рисунке 29. Сила $F$ приложена по направлению нити к одному из тел массы $m$. Участки нити по обе стороны от лёгкого блока, прикреплённого к телу массы $M$ параллельны.

  Решение. Силы, действующие на тела, изображены на рисунке 30.

  

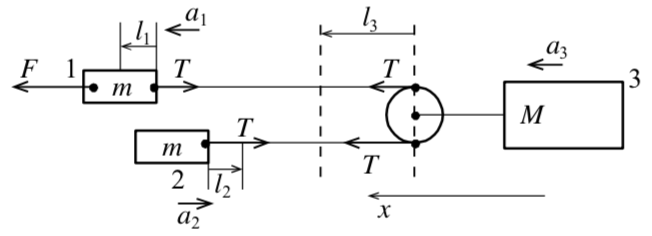
  Рис. 30

  Для первого тела:

  $Ox: \quad F - T = m a_1$.

  Для второго тела:

  $Ox:\quad -T = -ma_2$.

  Для третьего тела:

  $Ox:\quad 2T = Ma_3$.

  Т. к. нить нерастяжима, то смещение второго тела к блоку $(l_2)$ равно смещению первого тела от блока $(l_1)$. Т. к. блок сам смещается с ускорением, то к смещению первого блока добавится смещение $2l_3$:

  $a_1 = a_2 + 2a_3$.

  Из (2) и (3) следует $a_1 = a_3\frac{M}{2m}$.

  Тогда, решая совместно (1), (4) и (2), получим:

  $a_3 = \frac{F}{M+2m}$,

  тогда

  $a_2 = \frac{F}{(M+2m)}\cdot\frac{M}{2m}\ и\ a_1 = \left(\frac{F}{M+2m}\right)\left(\frac{M+4m}{2m}\right)$.

• 
  Сила трения

  • 16 ноября 2017 г.
  • 0 комментариев
  • 65525 просмотров

  Сила трения – сила механического сопротивления, возникающая в плоскости соприкосновения двух прижатых друг к другу тел при их относительном перемещении.

  Сила сопротивления, действующая на тело, направлена противоположено относительному перемещению данного тела.

  Сила трения возникает по двум причинам: 1) первая и основная причина заключается в том, что в местах соприкосновения молекулы веществ притягиваются друг к другу, и для преодоления их притяжения требуется совершить работу. Соприкасающиеся поверхности касаются друг друга лишь в очень небольших по площади местах. Их суммарная площадь составляет $0,01 \div 0,001$ от общей (кажущейся) площади соприкосновения. При скольжении площадь реального соприкосновения не остается неизменной. Сила трения (скольжения) будет изменяться в процессе движения. Если тело, которое скользит, прижать сильнее к телу, по которому происходит скольжение, то вследствие деформации тел площадь пятен соприкосновения (и сила трения) увеличится пропорционально прижимающей силе.

  $$F_\text{тр} \sim F_\text{приж}$$

  2) вторая причина возникнове ния силы трения – это наличие шероховатостей (неровностей) поверхностей, и деформация их при движении одного тела по поверхности другого. Глубина проникновения (зацепления) шероховатостей зависит от прижимающей силы, а от этого зависит и величина деформаций. Последние, в свою очередь, определяют величину силы трения: $F_\mathrm{тр} \sim F_\mathrm{приж}$.

  При относительном скольжении обе причины имеют место, потому характер взаимодействия имеет вид простого соотношения:

  $\boxed{F_\mathrm{тр} =\mu N}\ -$сила трения скольжения (формула Кулона - Амонтона), где

  $\mu\ -$ коэффициент трения скольжения,

  $N\ -$ сила реакции опоры, равная прижимающей силе.

  Величина коэффициента трения различна для разных комбинаций трущихся веществ даже при одинаковой их обработке (силы притяжения и упругие свойства зависят от рода вещества).

  Если между трущимися поверхностями будет находится смазка, то сила притяжения изменится заметным образом (будут притягиваться другие молекулы, и сила трения скольжения частично заменится силой вязкого трения, которую мы рассмотрим ниже).

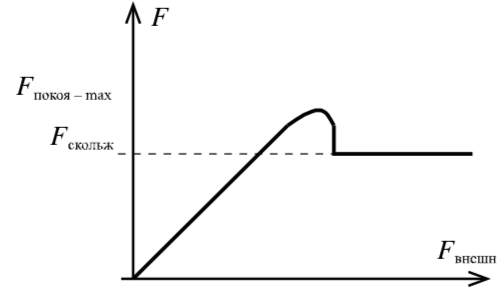
  Если на тело, лежащее на горизонтальной поверхности, действует горизонтальная сила $\vec F$, то движение будет вызвано этой силой только в том случае, когда она станет больше некоторого значения $(\mu N)$. До начала движения внешняя сила скомпенсирована силой трения покоя.

  
  

  










  Рис. 13

  Сила трения покоя всегда равна внешней силе, параллельной поверхности, и возникает по причине притяжения между молекулами в областях пятен соприкосновения и деформации шероховатостей.

  Сила трения покоя различна в разных участках поверхности по которой будет происходить движение. Если тело долго лежит на поверхности, то вследствие вибраций (они всегда присутствуют на поверхности Земли) площадь пятен соприкосновения незначительно увеличится. Поэтому для начала движения придётся преодолеть немного большую силу трения, чем сила трения скольжения. Данное явление называется явлением застоя. С этим явлением мы сталкиваемся, например передвигая мебель в комнате. (На рисунке 13 превосходство трения покоя над трением скольжения сильно преувеличено).

  Силой трения покоя мы пользуемся для перемещения на лыжах или просто при ходьбе.

  Рассмотренные виды силы трения относятся к сухому трению или внешнему. Но есть еще один вид силы трения – вязкое трение.

  При движении тела в жидкости или газе происходят достаточно сложные процессы обмена молекулами между слоями обтекающей жидкости или газа. Эти процессы называют процессами переноса.

  При небольших скоростях движения тела относительно газа или жидкости сила сопротивления будет определяться выражением:

  $\boxed{F_\mathrm{тр} = 6\pi \eta r v}\ -$ закон Стокса для шара, где

  $\eta\ -$ вязкость вещества, в котором движется тело;

  $r\ -$ средний поперечный размер (радиус) тела;

  $v\ -$ относительная скорость тела;

  $6\pi\ -$ коэффициент, соответствующей сферической форме тела.

  Вывод о величине скорости (большая она или маленькая) можно сделать, определив безразмерный коэффициент, называемый числом Рейнольдса:

  $\boxed{Re = \frac{\rho r v}{\eta}}\ -$ число Рейнольдса, где

  $\rho\ -$ плотность вещества, в которой движется тело.

  Если $Re < 1700$, то движение газа (жидкости) вокруг тела ламинарное (слоистое), и скорости можно считать малыми.

  Если $Re > 1700$, то движение газа (жидкости) вокруг тела турбулентное (с завихрениями), и скорости можно считать большими.

  В последнем случае на образование вихрей тратится большая часть кинетической энергии тела, а значит, сила трения становится большей, а зависимость перестаёт быть линейной.

  $\boxed{F_\mathrm{тр} = kv^2\rho S}\ -$ сила вязкого трения при больших скоростях, где

  $S\ -$ площадь поперечного сечения тела,

  $k\ -$ постоянная величина, зависящая от поперечных размеров тела.

  Часто последнюю формулу можно видеть в виде:

  \[F_\text{тр} = \beta v^2.\]

  Число Рейнольдса, выбранное равным $1700$, в действительности определяется конкретной задачей (условиями) и может принимать другие значения того же порядка. Объясняется это тем, что зависимость силы вязкого трения от скорости носит сложный характер: при некотором значении скорости линейная зависимость начинает нарушаться, а при некотором значении скорости эта зависимость становится квадратичной. 

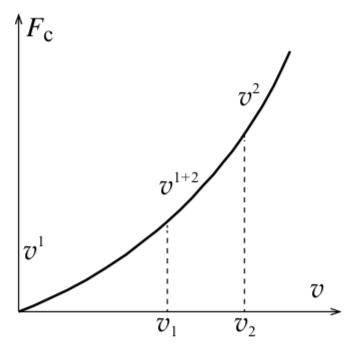  Рис. 14

  В промежутке от $v_1$ до $v_2$ степень принимает дробные значения (рис. 14) . Число Рейнольдса характеризует состояние динамической системы, при котором движение слоёв остаётся ламинарным, и сильно зависит от внешних условий. К примеру: стальной шар, двигаясь в воде вдали от границ жидкости (в океане, озере) сохраняет ламинарным движение слоёв при $Re = 1700$, а тот же шар, движущийся в вертикальной трубе немного большего, чем шар, радиуса, заполненной водой, уже при $Re=2$ вызовет появление завихрений воды вокруг шара. (Отметим, что число Рейнольдса не единственное, применяемое для описания подобного движения. Например, применяют ещё числа Фруда и Маха.)

  Из-за такой сложной зависимости силы сопротивления от размеров, формы тела и его скорости рассчитать с необходимой точностью силу сопротивления невозможно. Потому приходится создавать макеты летательных аппаратов и измерять силу сопротивления опытным путём, продувая воздух в аэродинамических трубах.

  Пример 7. Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению скорости на радиус капель: $F = krv$. Капли радиуса $0,1\ \text{мм}$, падая с большой высоты, у земли имеют скорость около $1\ \mathrm{м}/\mathrm{с}$. Какую скорость будут иметь капли, радиус которых в два раза меньше? В десять раз меньше?

  Решение: Капля падает с постоянной скоростью, т. к. сила тяжести скомпенсирована силой вязкого трения о воздух: $krv = mg$ или $krv = \rho \frac 43 \pi r^3 g$, откуда $v = \frac{4\rho\pi g}{3k}r^2$.

  Из полученного результата следует, что скорость капли прямо пропорциональна квадрату радиуса. Если радиус капли уменьшится в два раза, то скорость её падения уменьшится в четыре раза, и составит $v_1 \approx 0,25\ \text{м}/\text{с}$; а если радиус окажется в десять раз меньше, то скорость будет в сто раз меньше, т. е. $v_2 \approx 0,01\ \mathrm{м}/\mathrm{с}$.

  Задача любопытна тем, что может объяснить почему облака не падают. Ведь облака – это туман, который не падает из-за наличия восходящих потоков воздуха. На нижней границе облака находятся наиболее крупные капли. Поднимаясь, скорость потока уменьшается, т. к. он совершает работу над встретившимся воздухом и увеличивает свою потенциальную энергию. Раз скорость потока в верхней части облака меньше, то и размер капель там тоже меньше. Капли «висят» над поверхностью земли на постоянной высоте.

  
  

  
  

• 
  Закон всемирного тяготения. Вес тела

  • 16 ноября 2017 г.
  • 0 комментариев
  • 44550 просмотров

  Анализируя законы Кеплера, описывающие движение планет, И. Ньютон в 1667 году пришёл к открытию закона всемирного тяготения:

  \[\boxed{F = G \frac{mM}{r^2}},\]

  где $G\ -$ гравитационная постоянная.

  Все тела во Вселенной взаимно притягиваются друг к другу с силами прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними.

  В такой форме закон справедлив только для двух тел, которые можно считать материальными точками. Однако можно доказать, что для двух однородных тел шарообразной формы эта форма записи закона тоже справедлива.

  Измерить величину гравитационной постоянной удалось английскому физику Г. Кавендишу в 1798 году.

  С помощью крутильных весов и свинцовых шаров ему удалось получить значение гравитационной постоянной:

  \[\boxed{G = 6,67259 \cdot 10^{-11}\ \frac{\mathrm{Нм}^2}{\mathrm{кг}^2}}.\]

  Второй закон Ньютона позволяет записать для силы, с которой тело притягивается к Земле: $F = G\frac{Mm}{R^2} = mg$, тогда $\boxed{g = G\frac{M}{R^2}}\ -$ ускорение свободного падения на поверхности Земли (измерено Галилеем и Ньютоном), на расстоянии, большем радиуса на величину $h$, ускорение свободного падения находится по формуле:

  $\boxed{g = G \frac M{(R+h)^2}}\ -$ ускорение свободного падения на высоте $h$ от поверхности Земли.

  Силой тяжести называют силу, с которой тело притягивается к планете:

  \[\boxed{F = mg} - \mathrm{сила}\ \mathrm{тяжести}\]

  Рассмотрим твёрдое тело, расположенное на горизонтальной неподвижной опоре: под действием силы тяжести тело деформируется. Если тело находится на опоре, то на нижний слой действуют все верхние слои, и, как следствие, этот слой деформируется наибольшим образом. На предпоследний слой действует меньшее количество слоёв, и он деформируется меньше. Таким образом, тело, бывшее прямоугольным, примет вид трапеции. Нижний слой приблизился при такой деформации к центру тела, а значит, возникла сила упругости, направленная в сторону, противоположную направлению смещения частиц при деформации. Сила упругости, возникшая внутри данного тела, направлена перпендикулярно опоре. Эту силу, созданную деформированным телом и приложенную к опоре, называют весом тела. Опора под действием веса деформируется. Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры $N$ (от слова normal - перпендикуляр).










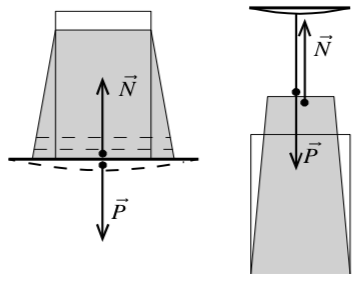  Рис. 9

  На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.

  Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы – силы тяготения.

  Невесомостью называют состояние тела, когда оно движется под действием только силы тяготения.

  Так же легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.

  Рассмотрим движение тела, помещённого в лифт. Пусть сам лифт движется с ускорением $\vec a$. Такое ускорение будет в двух случаях: 1) лифт поднимается равно ускорено, 2) лифт опускается равнозамедленно. Второй закон Ньютона для данного тела примет вид:








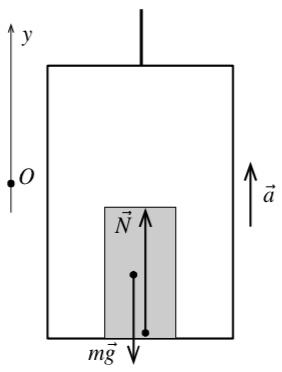  Рис. 10

  $\vec N + m \vec g = m \vec a.$

  При рассмотрении данного движения из лабораторной неподвижной системы отсчёта $Oy$ увидим, что в проекции на вертикальную ось $Oy$ второй закон запишется следующим образом:

  $N - mg = ma,$

  откуда 

  $N = ma + mg = m(g+a).$

  Но по третьему закону Ньютона знаем, что сила реакции опоры и вес тела равны и противоположны, следовательно:

  $N = P,$

  тогда: $\boxed{P = m(g+a)}\ -$ вес тела, движущегося с ускорением, направленным вверх (рис. 10).

  Не трудно проследить за тем, что мы получим, если ускорение тела будет направлено вниз.

  В проекции на ось $Oy$ ускорение проецируется со знаком <<$-$>>, что даст окончательную формулу для веса:

  $\boxed{P = m(g-a)}\ -$ вес тела, движущегося с ускорением, направленным вниз.

  Или в общем случае: $\boxed{P = m(g \pm a)}\ -$ вес тела, движущегося с ускорением.







  Рис. 11а

  Подобным образом можно получить выражение для веса тела, движущегося равномерно по выпуклому участку дороги.

  $\boxed{P = m(g-a) = m(g - \frac{v^2}{R})}\ -$ вес тела, движущегося с ускорением, направленным вниз (выпуклая дорога).

  $\boxed{P = m(g+a) = m(g+ \frac{v^2}{R})}\ -$ вес тела, движущегося с ускорением, направленным вверх (вогнутая дорога).

  Важное дополнение:

  Для рассматриваемой силы, называемой весом, важно понимать и уметь правильно изображать точку приложения этой силы.








  На рисунке 11а показан лифт, у которого нет ускорения. Тогда сила тяжести равна силе реакции опоры . А по третьему закону Ньютона, сила реакции опоры равна весу тела. Точка приложения силы тяжести расположена в геометрическом центре тела, если тело однородно и правильной формы. Точка приложения силы реакции опоры должна быть изображена внутри тела вблизи с нижней поверхностью тела на линии действия силы тяжести. Последнее свойство на рисунке не выдержано для удобства изображения (иначе силы на рисунке будут накладываться друг на друга). Точка приложения веса тела находится внутри опоры (пола лифта) вблизи поверхности на линии действия силы реакции опоры.










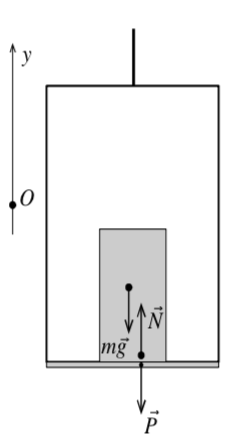
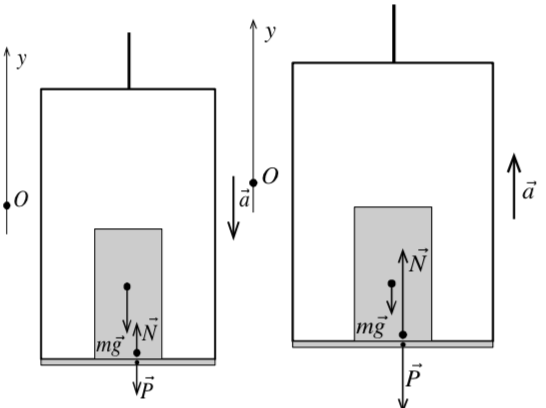  Рис. 11б                                    Рис. 11в

  
  

  На рисунке 11б ускорение лифта направлено вниз. Тогда сила реакции опоры меньше силы тяжести . А вес снова равен силе реакции опоры.

  На рисунке 11в ускорение лифта направлено верх. Тогда сила реакции опоры больше силы тяжести . А вес снова равен силе реакции опоры.

  Пример 5. Определить среднюю плотность Солнца, если его масса равна $2\cdot 10^{30}\ \text{кг}$, а ускорение свободного падения на поверхности приблизительно составляет $273,1\ \text{м}/\text{с}^2$.

  Решение. Так как $g = G\frac{M}{R^2}$, то можем найти радиус Солнца: $R = \sqrt{\frac{GM}{g}}$. Считая Солнце шаром найденного радиуса и известной массы, можем найти среднюю плотность.

  \[\rho = \frac MV = \frac{M}{\frac 43 \pi R^3} = \frac{3M}{4\pi \left(\frac{GM}{g}\right)^{\frac 32}} = \frac{3}{4\pi \sqrt M}\left(\frac gG\right)^{\frac 32}.\]

  Количественно ответ будет таким: $\rho = 1400\ \text{кг}/\text{м}^3$. Однако следует отметить, что этот ответ таков в данной модели. В действительности плотность Солнца не одинакова в недрах светила, и является функцией расстояния от центра. Мы же посчитали её везде одинаковой.








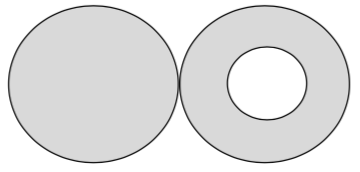  Рис. 12

  Пример 6. На сколько изменится сила притяжения двух одинаковых шаров, изготовленных из одинакового вещества плотностью $\rho$, если у одного из них создать полость сферической формы, расположенную внутри одного из них в его центре? Изначально шары касались друг друга и притягивались с силой $80\ \text{Н}$. Радиус полости равен половине радиуса шара (рис. 12).

  Решение. Сила взаимодействия определяется законом всемирного тяготения. Т. к. формы тел шарообразные, то мы можем применить известную формулу закона: $F_1 = G\frac{Mm}{R^2}$.

  Массы тел равны, обозначим их $m$, Масса извлечённой части $m_0 = \frac 43 \pi (\frac{R}{2})^3 \rho = \frac 18 m$. Новая сила будет меньше первоначальной на величину силы взаимодействия извлечённой части с первым шаром (принцип суперпозиции сил). Следовательно:

  \[F_2 = G\frac{m_0 m}{(2R)^2} = G\frac{\frac 18 mm}{(2R)^2} = \frac 18 F\frac{mm}{(2R)^2} = \frac 18 F = 10\ \text{Н}.\]

  Сила притяжения шаров станет меньше на $10\ \text{Н}$, следовательно, станет равной $70\ \text{Н}$.

• 
  Взаимодействие тел, третий закон Ньютона

  • 16 ноября 2017 г.
  • 0 комментариев
  • 58555 просмотров

  Из анализов многочисленных опытов, как уже отмечалось, было получено соотношение масс взаимодействующих тел и их ускорений:

  \[\frac{m_2}{m_1} = \frac{a_1}{a_2},\quad или \quad m_1a_1 = m_2a_2.\]

  Но мы знаем из опытов, что при взаимодействии всегда ускорения тел противоположны друг другу: $\vec a_1 \uparrow \downarrow \vec a_2$, следовательно, $m_1\vec a_1 = - m_2 \vec a_2$.

  Но произведение массы тела на ускорение этого тела равна действующей на это тело силе. Тогда 

  $\boxed{\vec F_1 = -\vec F_2}$.

  Данное утверждение и представляет собой третий закон Ньютона.

  Третий закон Ньютона: При взаимодействии тела действуют друг на друга с силами, равными по величине, противоположными по направлению, одинаковыми по природе и лежащими на прямой, проходящей через центры тел.

  Данные проявления встречаются всюду:

  1) при столкновении (упругом или неупругом) тела деформируются, при этом появляются силы упругости. Первое тело действует на второе с силой $F_{21}$, а второе на первое с силой $F_{12}$. Причём обе силы по природе своей являются силами упругости – силами взаимодействия между молекулами (электромагнитными). Силы лежат на одной прямой, лежащей на линии точек приложения сил. Силы противоположны.

  2) при гравитационном взаимодействии двух тел (Земля и Луна, или Солнце и Юпитер и т. д.) возникают две гравитационные силы, которые тоже противоположны и равны друг другу.

  3) при взаимодействии прямоугольного тела, стоящего на поверхности стола, то же возникают две силы упругости: сила возникает потому, что стол деформировался (прогнулся, деформация изгиба см. далее), а сила возникает потому, что прямоугольное тело тоже деформировалось (сжалось под действием силы тяжести, подробнее см. далее). Обе силы равны друг другу и противоположны.

  Рассмотрение примеров позволяет сформулировать следующие свойства сил, возникающих при взаимодействии:

  силы всегда появляются (или исчезают) парами;

  силы не компенсируют друг друга, т. к. приложены к разным телам;

  силы одинаковой природы.

  Пример 3. Для растяжения пружины жёсткостью $50\ \mathrm{Н}/\mathrm{м}$, закреплённой одним концом на стене, на $20\ \mathrm{см}$ требуется сила $10\ \mathrm{Н}$. Какую силу нужно приложить к этой пружине, чтобы растянуть её на $20\ \mathrm{см}$, прикладывая силу с двух сторон и действуя в противоположных направлениях?

  Решение.  В первом случае в растянутом состоянии пружина находилась в состоянии покоя. Следовательно, по второму закону Ньютона сила, приложенная к пружине со стороны руки, скомпенсирована силой, приложенной к пружине со стороны стены. Значит, стена действует на пружину с силой $10\ \mathrm{Н}$. а) Первая пара сил: точка приложения силы со стороны руки неподвижна и находится в пружине, а сила упругости пружины приложена к точке, находящейся в руке, и тоже неподвижна. Эти две силы равны и противоположны по третьему закону Ньютона. б) Вторая пара сил: во второй паре взаимодействующих тел (стены и пружины) силы тоже равны и противоположны по тому же закону.

  Во втором случае пружина тоже находится в покое. Только теперь одна из сил создаётся одной рукой, а вторая сила второй рукой. Сила, создаваемая стеной в первом случае, заменяется силой, создаваемой второй рукой, во втором. Понятно, что неподвижной пружина останется во втором случае только тогда, когда величина силы тоже сохранит первоначальное значение. Следовательно, во втором случае к пружине нужно приложить силу $10\ \mathrm{Н}$ с обеих сторон.

• 
  Сила, второй закон Ньютона

  • 16 ноября 2017 г.
  • 0 комментариев
  • 231386 просмотров

  Сила является мерой взаимодействия (взаимного действия). Если действие велико (мало), то говорят о большой (малой) силе. Сила обозначается буквой $$F$$ (первая буква слова force).

  При взаимодействии чем больше сила, тем больше ускорение тела, на которое эта сила действует. Следовательно, ускорение прямо пропорционально действующей силе: $a\sim F$.

  Но уже говорилось о том, что ускорение зависит от массы тела: $a \sim \frac 1m$

  Обощая эти зависимости получим:

  \[a = \frac{F}{m}, \quad \mathrm{или}\quad F = ma.\]

  Теперь рассмотрим свойства силы, устанавливаемые опытным путём:

  1) Результат действия (проявления) силы зависит от направления действующей силы, следовательно, сила – величина векторная.

  2)  Результат действия (проявления) силы зависит от величины приложенной силы .

  3)  Результат действия (проявления) силы зависит от точки приложения силы.

  4) За единицу силы принято значение такой силы, которая вызывает ускорение $1\ \mathrm{м}/\mathrm{с}^2$ у тела массой $1\ \mathrm{кг}$. Единицу силы назвали в честь Исаака Ньютона 1 нью'тон. (Произносить фамилию считается правильным таким образом, как произносится фамилия в том государстве, где проживал или проживает учёный.)

  $[\overset{\rightarrow}{F}] = 1\ \mathrm{Н} = 1\ \mathrm{кг}\cdot\frac{\mathrm{м}}{\mathrm{с}^2}\quad \mathrm{(ньютон)}.$

  5) Если на тело одновременно действуют несколько сил, то каждая сила действует независимо от других. (Принцип суперпозиции сил). Тогда все силы необходимо сложить векторно и получить результирующую силу (рис. 4).

  
  

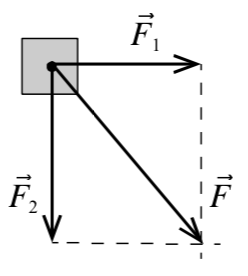  Рис. 4

  Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:

  Второй закон Ньютона: Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил:

  $\boxed{\sum \vec{F} = m\vec{a}}.$

  Данное выражение можно представить и в другой форме: так как $\vec a = \frac{\vec v_\mathrm{к} - \vec v_0}{t}$, то второй закон Ньютона примет вид: $\sum \vec F = m\frac{\vec v_\mathrm{к} - \vec v_0}{t}$.

  Произведение массы тела и его скорости называют импульсом тела:

  $\vec p = m\vec v$,

  тогда получим новое выражение для второго закона Ньютона:

  $\boxed{\sum \vec F = \frac{m\vec v_\mathrm{к} - m\vec v_0}{t}} = \frac{\vec p_\mathrm{к} - \vec p_0}{t} = \frac{\Delta \vec p}{t}$.

  $\boxed{\sum \vec F = \frac{\vec p_\mathrm{к} - \vec p_0}{t}}$ $-$ второй закон Ньютона в импульсной форме для среднего значения силы. Здесь $\vec p_\mathrm{к} - \vec p_0 = \Delta \vec p$ $-$ изменение импульса тела, $t\ -$ время изменения импульса тела.

  $\boxed{\sum \vec F = \frac{d\vec p}{dt}}\ -$ второй закон Ньютона в импульсной форме для мгновенного значения силы.

  Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:

  $\boxed{\vec a = \sum \vec a_i = \vec a_1 + \vec a_2 + \dots + \vec a_i = \frac{\sum \vec F}{m} = \frac{\vec F_1 + \vec F_2 + \dots + \vec F_i}{m} = \frac{\vec F_1}{m} + \frac{\vec F_2}{m} + \dots + \frac{\vec F_i}{m}}$.

  Первая форма записи второго закона $(\sum \vec F = m\vec a)$ справедлива только при малых скоростях по сравнению со скоростью света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Так же следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.

  Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.

  Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.


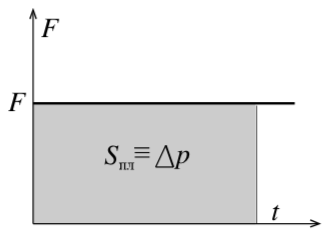  Рис. 5

  Иногда очень полезно знать, что произведение $\vec F \cdot t$ называют импульсом силы, и его значение $\vec F \cdot t = \Delta \vec p$ равно изменению импульса тела.

  Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).

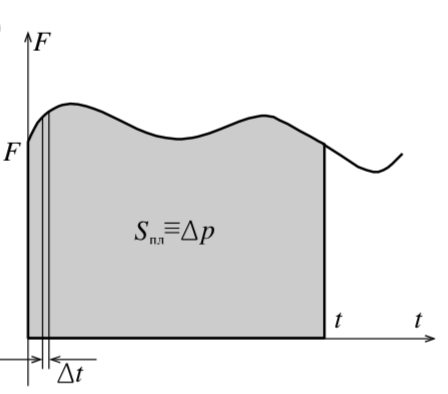
  Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы $\Delta t$ такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:

  Площадь фигуры под графиком $F(t)$ численно равна изменению импульса.

  В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.

  Рис. 6

  Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс.









  Неразличимость гравитационной и инертной масс означает, что и ускорения, вызванные гравитационным взаимодействием (законом всемирного тяготения) и любым другим тоже неразличимы.

  Пример 2. Мяч массой $0,5\ \mathrm{кг}$ после удара, длящегося $0,02\ \mathrm{с}$, приобретает скорость $10\ \mathrm{м}/\mathrm{с}$. Найти среднюю силу удара.

  Решение. В данном случае рациональнее выбрать второй закон Ньютона в импульсной форме, т. к. известны начальная и конечная скорости, а не ускорение, и известно время действия силы. Также следует отметить, что сила, действующая на мяч, не остаётся постоянной. По какому закону меняется сила со временем, неизвестно. Для простоты мы будем пользоваться предположением, что сила постоянная, и её мы будем называть средней.

  Тогда $\sum \vec F = \frac{\Delta \vec p}{t}$, т. е. $\vec F_\mathrm{ср}\cdot t = \Delta \vec p$. В проекции на ось, направленной вдоль линии действия силы, получим: $F_\mathrm{ср}\cdot t = p_\mathrm{к}-p_0 = mv_\mathrm{к}$. Окончательно для искомой силы получим:

  \[F_\mathrm{ср} = \frac{mv_\mathrm{к}}{t}.\]

  Количественно ответ будет таким: $F_\mathrm{ср} = \frac{0,5\ \mathrm{кг}\cdot 10\ \frac{\mathrm{м}}{\mathrm{с}}}{0,02\ \mathrm{с}} = 250\ \mathrm{Н}$.

• 
  Взаимодействие тел, инертность, масса

  • 15 ноября 2017 г.
  • 0 комментариев
  • 109472 просмотра

  Из наблюдений можно заметить, что тела изменяют свою скорость только при наличии не скомпенсированного действия. Т. к. быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.

  Установились считать: чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.

  Инертность – это свойство тела сохранять свою скорость постоянной (то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.

  Например, движущийся по дороге автомобиль не может мгновенно остановиться, для уменьшения скорости требуется некоторое время, а за это время он успевает переместиться на довольно большое расстояние (десятки метров). (Осторожно переходите дорогу!!!)

  Мерой инертности является инертная масса.

  Масса (инертная) – мера инертности тела.

  Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение: $\boxed{a\sim\frac 1m}$.

  Данная зависимость записана единственно правильным способом, т. к. форма $m \sim \frac 1a$ не верна. Масса не может зависеть от ускорения, она является свойством тела, а ускорение является характеристикой состояния движения тела.

  Данная зависимость подтверждается многочисленными опытными результатами.

  

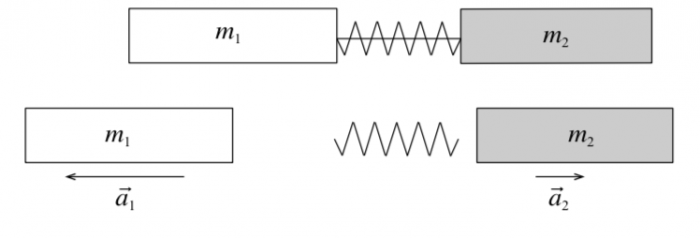
  Рис. 2 Измерение массы методом взаимодействия тел.

  Два тела, скреплённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться не которое время с ускорением (рис. 1) . Опыт показывает, что при любых взаимодействиях данных двух тел отношение ускорений тел равно обратному отношению их масс:

  \[\frac{a_1}{a_2} = \frac{m_2}{m_1};\]

  если взять первую массу за эталонную ($m_1 = m_\mathrm{эт}$), то $m_2 = m_\mathrm{эт}\frac{a_\mathrm{эт}}{a_2}$.

  Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной.

  Измерение массы методом взвешивания тел.

  Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы (рис. 2).

  

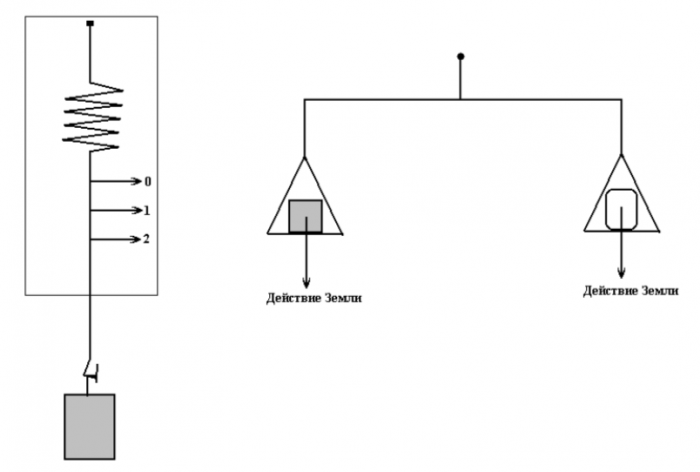
  Рис. 2

  Рис. 3

  Масса, измеренная путём взвешивания, называется гравитационной.

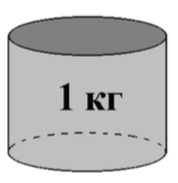
  В качестве эталона и той и другой массы принята масса тела, выполненного в форме цилиндра высотой $39\ \mathrm{мм}$ и диаметром $39\ \mathrm{мм}$, изготовленного из сплава 10 % иридия и 90 % платины (рис. 3).

  В 1971 г наши соотечественники Брагинский и Панов придумали и провели опыт по сравнению массы гравитационной и инертной. Оказалось, что с точностью до $10^{-12}$ % эти массы равны.

  Данный факт известен был и ранее, и послужил основанием для формулировки Эйнштейном принципа эквивалентности.

  Принцип эквивалентности утверждает, что

  1) ускорение, вызванное гравитационным взаимодействием в малой области пространства, и за небольшой интервал времени, неотличимо от ускоренно движущейся системы отсчёта.

  2) ускоренно движущееся тело эквивалентно неподвижному телу, находящемуся в гравитационном поле.

  Пример 1. 

  Два тела массами $400\ \mathrm{г}$ и $600\ \mathrm{г}$ двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью $3\ \mathrm{м}/\mathrm{с}$?

  Решение. 

  Сила, возникающая при взаимодействии тел, конечно же, не остаётся постоянной, и ускорения тоже. Мы будем считать, что и силы, и ускорения принимают некоторы е средние значения, причём одинаковые для любого момента времени. Отношение ускорений тел равно обратному отношению их масс: $\frac{a_1}{a_2} = \frac{m_2}{m_1}$. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:

  \[\frac{m_2}{m_1} = \frac{a_1}{a_2} = \frac{\frac{\Delta v_1}{\Delta t}}{\frac{\Delta v_2}{\Delta t}} = \frac{v_\mathrm{к1}-v_{01}}{v_\mathrm{к2}-v_{02}} = \frac{v_{01}}{v_{02}},\]

  откуда получим искомую скорость: $v_{02} = \frac{m_1}{m_2}\cdot v_{01}.$

  Количественно ответ будет таким: $v_{02} = \frac{0,4\ \mathrm{кг}}{0,6\ \mathrm{кг}}\cdot 3\ \frac{\mathrm{м}}{\mathrm{с}} = 2\ \frac{\mathrm{м}}{\mathrm{с}}$.

  
  

• 
  6. Закон Архимеда

  • 22 августа 2017 г.
  • 3 комментария
  • 3133 просмотра

  На поверхности твёрдого тела, погружённого в жидкость (газ), действуют силы давления.

• 
  11-М-1. 2. Иррациональные неравенства

  • 13 июля 2017 г.
  • 0 комментариев
  • 7243 просмотра

  Иррациональными называют неравенства, в которых переменные входят под знаком корня. Так как корень чётной степени существует только у неотрицательных чисел, то при решении неравенств, содержащих такое выражение, прежде всего удобно найти ОДЗ.

  Пример 3 (МГУ, 1998)

  Решите неравенство `sqrt(x + 3) > x + 1`.

  Решение

  Это неравенство можно решить несколькими способами. Решим его графически (рис. 1). Построим графики функций `y = sqrt(x + 3)`,  `y = x + 1` и  посмотрим, где первый график расположен выше второго. Для нахождения решения останется решить       только       уравнение `sqrt(x + 3) = x + 1` (и не надо рассматривать случаи разных знаков для `x + 1`!).

  $\sqrt{x+3}=x+1\Leftrightarrow\left\{\begin{array}{l}x+1\geq0,\\x+3=x^2+2x+1\end{array}\Leftrightarrow x=1\Rightarrow x\in\lbrack-3;1).\right.$

  Ответ:

  `[- 3; 1)`.

  Сначала приведём уже выведенные в 10-ом классе условия равносильности для уравнений (в частности, для того, чтобы была понятна приве-дённая уже здесь нумерация условий равносильности для корней `(`УР К`)`):

  `sqrt(f(x)) = a^2 iff f(x) = a^4`.	(УР К1)
  $\sqrt{f\left(x\right)}=g\left(x\right)\Leftrightarrow\left\{\begin{array}{l}g\left(x\right)\geq0,\\f(x)=g^2(x).\end{array}\right.$	(УР К2)
  $\sqrt{f(x)}=\sqrt{g(x)}\overset{ОДЗ}\Leftrightarrow f(x)=g(x).$	(УР К3)
  $\begin{array}{l}\sqrt{f(x)}=\sqrt{g(x)}\Leftrightarrow\left\{\begin{array}{l}f(x)=g(x),\\\left[\begin{array}{l}f(x)\geq0,\\g(x)\geq0.\end{array}\right.\end{array}\right.\\\end{array}$	(УР К4)

  
  

  ПУНКТ 1. НЕРАВЕНСТВА ВИДА `sqrt(f(x)) >= g(x)` и `sqrt(f(x)) <= g(x)`

  ОДЗ: `f(x) >= 0`.

   Рассмотрим неравенство `sqrt(f(x)) >= g(x)`.  Докажем, что

  (УР К5)

                                                                               

  Доказательство

  1. Если  является решением неравенства `sqrt(f(x)) >= g(x)`, то `f(x) >= 0` и `sqrt(f(x))` существует. При этом неравенство заведомо выполнено при `g(x) < 0`.  Если же `g(x) >= 0`, то возведение в квадрат обеих частей неравенства приводит к равносильному неравенству `f^2 (x) >= g^2 (x)`. 

  2. Пусть теперь `x` является решением совокупности неравенств       

  
  

  Тогда:

  а) если `g(x) < 0`  и  `f(x) >= 0`, то существует `sqrt(f(x))` и заведомо выполнено неравенство `sqrt(f(x)) >= g(x)`:

  б) если `g(x) >= 0`  и  `f(x) - g^2 (x) >= 0 iff (sqrt(f(x)) - g(x)) (sqrt(f(x)) + g(x)) >= 0`,

  то `f(x) - g^2 (x) >= 0 iff sqrt(f(x)) - g(x) >= 0`.

  Можно ОДЗ неравенства найти отдельно, тогда условие равносильности примет вид:

  (УР К6)

                                                              

  Теперь рассмотрим неравенство вида  `sqrt(f(x)) <= g(x)`.  Докажем, что

  $\sqrt{f(x)}\leq g(x)\Leftrightarrow\left\{\begin{array}{l}g(x)\geq0,\\f(x)\leq g^2(x),\\f(x)\geq0.\end{array}\right.$

  (УР К7)

                                                                

  Доказательство

  1. Если `x` является решением неравенства `sqrt(f(x)) <= g(x)`, то  `f(x) >= 0` и существует `sqrt(f(x))`, а тогда `g(x) >= 0`, и возведение в квадрат обеих частей неравенства приводит к равносильному неравенству `f(x) <= g^2 (x)`.

  2.  Если `x` является решением системы неравенств   $\left\{\begin{array}{l}g(x)\geq0,\\f(x)\leq g^2(x),\\f(x)\geq0,\end{array}\right.$   то `f(x) >= 0` и существует `sqrt(f(x))`,     а тогда `f(x) - g^2 (x) <= 0 iff (sqrt(f(x)) - g(x))(sqrt(f(x)) + g(x)) <= 0`. Но, по условию, `g(x) >= 0`, поэтому `f(x) - g^2 (x) <= 0 iff sqrt(f(x)) - g(x) <= 0`.

  Пример 4 (МФТИ, 1998)

  Решите неравенство `3 sqrt(3x^2 -8x - 3) > 1 - 2x`.

  
  

  Решение

  Первый способ

  Воспользуемся (УР К6): 

  
  

  Ответ

  `(- oo ;  (34 - 30 sqrt2)/(23)) uu [3; + oo)`.

  
  

  Второй способ

  Можно оформить решение неравенства и несколько по – другому. Найдём сначала ОДЗ:

  
  

• 
  11-М-1. 1 Равносильность уравнений и неравенств

  • 13 июля 2017 г.
  • 0 комментариев
  • 8794 просмотра

  В нашем задании большую роль  будет играть понятие  равносильности.

  Два неравенства    

  `f_1 (x) > g_1 (x)`   и   `f_2 (x) > g_2 (x)`

  (1)

  или два уравнения

  `f_1 (x) = g_1 (x)`   и   `f_2 (x) = g_2 (x)`

  (2)

  называются равносильными на множестве `X`, если каждое решение первого неравенства (уравнения), принадлежащее множеству `X`, является решением второго и, наоборот, каждое решение второго, принадлежащее `X`, является решением первого, или, если, ни одно из неравенств (уравнений) на `X` не имеет решений. Т. е. два неравенства (уравнения) равносильны, по определению, если множества решений этих неравенств (уравнений) на `X` совпадают.

  Отсюда следует, что вместо того, чтобы решать данное неравенство (уравнение), можно решать любое другое, равносильное данному. Замену одного неравенства (уравнения) другим, равносильным данному на `X`, называют равносильным переходом на `X`. Равносильный переход обозначают двойной стрелкой `hArr`. Если уравнение `f(x) = 0`  (или неравенство) `f(x) > 0`) равносильно уравнению `g(x) = 0` (или неравенству `g(x) > 0`), то это мы будем обозначать так:  

  `f(x) = 0 hArr g(x) = 0`   (или `f(x) > 0 hArr g(x) > 0`).

  Пример 1

  `sqrt(x^2 -4) = 1 - x^2 hArr sqrt(sin ^2 x - 2) = 0`, т. к. ни то, ни другое не имеет решения.

  Важно понимать, что для доказательства неравносильности двух неравенств (уравнений) нет необходимости решать каждое из неравенств (уравнений), а затем убеждаться в том, что множества их решений не совпадают - достаточно указать одно решение одного из неравенств (уравнений), которое не является решением другого неравенства (уравнения).

  Пример 2

  При каких значениях параметра  `a` системы

  $\left\{\begin{array}{l}ax+3y=6a-4,\\x+y=2a\end{array}\right.$

  и

  $\left\{\begin{array}{l}x^2-2y^4-6x+8=0,\\x^2+y^2-\left(2a+4\right)x+2(a^2+a+2)=0\end{array}\right.$

  равносильны?

  
  

  Решение

  Решим сначала первую, более простую систему  

  $\left\{\begin{array}{l}ax+3y=6a-4,\\x+y=2a\end{array}\Leftrightarrow\left\{\begin{array}{l}y=2a-x,\\ax+3(2a-x)=6a-4\Leftrightarrow x(a-3)=-4\end{array}\Leftrightarrow\right.\right.$

  $\Leftrightarrow\left[\begin{array}{l}\left\{\begin{array}{l}a\neq3,\\x=-\dfrac4{a-3},\\y=2a+\dfrac4{a-3}=\dfrac{2a^2-6a+4}{a-3};\end{array}\right.\\\left\{\begin{array}{l}a=3,\\0\cdot x=-4\Leftrightarrow\varnothing.\end{array}\right.\end{array}\right.$

  Подставим  `a = 3` во вторую систему

  $a=3:\left\{\begin{array}{l}x^2-2y^4-6x+8=0,\\x^2+y^2-10x+28=0\Leftrightarrow\left(x-5\right)^2+y^2+3=0\Leftrightarrow\varnothing,\end{array}\Rightarrow\right.$

  При `a = 3` системы  равносильны,  т. к. при этом значении параметра обе системы не имеют решений.

  При `a = 3` первая система имеет единственное решение. Заметим, что во второй системе  входит только в четной степени, значит, если решением является пара `(x_0, y_0)`, то пара `(x_0 , -y_0)` тоже будет решением. При этом если `y_0 != - y_0 iff y_0 != 0`, то решений будет два. Следовательно, единственным решением может быть только пара `(x_0 , 0)`. Посмотрим, при каких `a` такое решение у системы есть. Подставим эту пару в систему

  $\left\{\begin{array}{l}x_0^2-6x_0+8=0\Leftrightarrow x_0=3\pm1,\\x_0^2-\left(2a+4\right)x_0+2\left(a^2+a+2\right)=0\end{array}\Leftrightarrow\left[\begin{array}{l}\left\{\begin{array}{l}x_0=2,\\a^2-a=0\Leftrightarrow a=\left[\begin{array}{l}0,\\1;\end{array}\right.\end{array}\right.\\\left\{\begin{array}{l}x_0=4,\\a^2-3a+2=0\Leftrightarrow a=\left[\begin{array}{l}2,\\1.\end{array}\right.\end{array}\right.\end{array}\right.\right.$

  Итак, таких  `a` три: `0, 1, 2`. Но при этих `a`  вторая система может иметь и другие решения, а если у неё других решений нет, то её единственное решение может не совпадать с решением первой системы, и тогда такое  `a` не удовлетворяет условию задачи. Проверим эти значения параметра.

  1. `a=0`: Первая система имеет решение: `x = 4/3` и `y = - 4/3 != 0`. Следовательно, системы не равносильны, т. к. решения систем не совпадают (у второй `y=0`).

  2. `a=1`: Вторая  система  имеет  вид 

  $\left\{\begin{array}{l}x^2-2y^4-6x+8=0,\\x^2+y^2-6x+8=0\end{array}\Leftrightarrow\left\{\begin{array}{l}y=0,\\x=3\pm1=4;2.\end{array}\right.\right.$

  Следовательно, системы не равносильны, т. к. вторая имеет два решения.

  3. $a=2:\left\{\begin{array}{l}ax+3y=6a-4,\\x+y=2a\end{array}\Leftrightarrow\left\{\begin{array}{l}x=4,\\y=0\end{array}\right.\right.$

  и $\left\{\begin{array}{l}x^2-2y^4-6x+8=0,\\x^2+y^2-\left(2a+4\right)x+2\left(a^2+a+2\right)=0\end{array}\Leftrightarrow\left\{\begin{array}{l}x^2-2y^4-6x+8=0,\\\left(x-4\right)^2+y^2=0\Leftrightarrow\left\{\begin{array}{l}x=4,\\y=0\end{array}\right.\end{array}\Leftrightarrow\left\{\begin{array}{l}x=4,\\y=0.\end{array}\right.\right.\right.$

  Следовательно, системы при этом значении  равносильны – они имеют единственное решение `(4; 0)`.

  
  

  Ответ

  `2; 3`.

  При решении неравенств и уравнений  часто используются следующие равносильные переходы.

  1. Если  функции  `f(x)`, `g(x)`, `h(x)` определены на множестве `X` , то на этом множестве 

  а)	`f(x) < g(x) iff f(x) + h(x) < g(x) + h(x)`.	(УР 1)
  б)	`f(x) = g(x) iff f(x) + h(x) = g(x) + h(x)`.	(УР 2)

                                                                                                                                         

  2. Если `h(x) > 0` на `X`, то на `X`

  `f(x) < g(x) iff f(x) h(x) < g(x) h(x)`,

  (УР 3)

   т. е. умножение неравенства на положительную функцию приводит к равносильному неравенству с тем же знаком.

  3. Если `h(x) < 0` на `X`, то на `X`

  `f(x) < g(x) iff f(x) h(x) > g(x) h(x)`,

  (УР 4)

   т. е. при умножении неравенства на отрицательную функцию знак неравенства меняется на противоположный.

  4. Если `h(x) != 0` на `X`, то на `X`

  `f(x) = g(x) iff f(x) h(x) = g(x) h(x)`.

  (УР 5)

  5. Если обе части неравенства неотрицательны на `X`, то возведение в квадрат обеих частей  приводит к равносильному неравенству, т. е.

  `f(x) < g(x) iff f^2 (x) < g^2 (x)`.

  (УР 6)

                                                                                     

  Если обе  части  неравенства отрицательны, то  умножив обе части на `(­–1)`, придём к неравенству противоположного знака, но с положительными частями, и к нему применим `(`УР `6)`.

  Если левая и правая части неравенства имеют разные знаки, то возведение в квадрат может привести как к верному, так и к неверному неравенству: `-4<5`; `16<25`; `-7<5`, но `49>25`, поэтому в этом случае нельзя возводить неравенство в квадрат.

  6. Если обе части уравнения неотрицательны, то

   

  `f(x) = g(x) iff f^2 (x) = g^2 (x)`.

  (УР 7)

  7. Для любых  `f(x)` и `g(x)` на `X` и любого натурального  `n`

  `f(x) = g(x) iff f^(2n + 1) (x) = g^(2n + 1) (x)`.

  (УР 8)

  
  

  8. Неравенство вида `f(x)>=0(<=0)` называется нестрогим. По определению,

  $f\left(x\right)\geq0\left(\leq0\right)\Leftrightarrow\left[\begin{array}{l}f\left(x\right)=0,\\f\left(x\right)>0\left(<0\right).\end{array}\right.$

  (УР 9)

  
  
• 
  11-М-1. Введение

  • 13 июля 2017 г.
  • 0 комментариев
  • 1944 просмотра

  Цель нашего задания - вспомнить основные правила и приемы решения алгебраических неравенств и систем уравнений. Многие из них  вам хорошо известны, некоторые покажутся новыми и, с первого взгляда, даже лишними, но не спешите их отбросить сразу - решите известную вам задачу разными способами и выберите сами тот способ, который вам больше нравится.

• 
  10-м-1. Вступление

  • 12 июля 2017 г.
  • 0 комментариев
  • 767 просмотров

  В нашем задании большую роль будет играть равносильность уравнений и систем. Поэтому коротко мы напомним основные понятия, связанные с этим.

  Неравенства – одна из важнейших тем в школьном курсе математики. Мы вспомним, прежде всего, метод интервалов для рациональных функций. Обратите внимание на то, как мы выделяем решение на числовой оси.

  Затем рассмотрим иррациональные уравнения и уравнения, содержащие модуль или квадратный корень. Приведём условия равносильности, которыми вы, наверное, пользуетесь, но не записываете в таком виде. Всё это даёт возможность решать уравнения быстрее, что важно для выполнения, например, заданий ЕГЭ.